练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    请用数学归纳法证明：1＋3＋6＋…＋＝(n∈N*)．

    答案：数学归纳法
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知an=
    1n(n+1)
    ，数列{an}的前n项的和记为Sn．
    （1）求S1，S2，S3的值，猜想Sn的表达式；
    （2）请用数学归纳法证明你的猜想．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    是否存在常数a，b，使等式
    12
    1×3
    +
    22
    3×5
    +…+
    n2
    (2n-1)(2n+1)
    =
    an2+n
    bn+2
    对于一切n∈N*都成立？若不存在，说明理由；若存在，请用数学归纳法证明？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知：函数f(x)=-
    1
    6
    x3+
    1
    2
    x2+x    ，x∈R．
    （Ⅰ）求证：函数f（x）的图象关于点A(1，
    4
    3
    )    中心对称，并求f（-2007）+f（-2006）+…+f（0）+f（1）+…+f（2009）的值．
    （Ⅱ）设g（x）=f′（x），an+1=g（an），n∈N+，且1＜a1＜2，求证：
    （ⅰ）请用数学归纳法证明：当n≥2时，1＜an＜
    3
    2
    ；
    （ⅱ）|a1-
    		2
    |+|a2-
    		2
    |+…+|an-
    		2
    |＜2    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•红桥区二模）已知数列{an}，{bn}，其中a1=p，b1=q，又an=pan-1，bn=qan-1+rbn-1（n≥2，n∈N+）（p、q、r为常数，且pqr≠0，p≠r）．
    （Ⅰ）写出b2，b3，b4（用p、q、r表示）；
    （Ⅱ）试推测出bn用p、q、r、n表示的公式；
    （Ⅲ）请用数学归纳法证明你（Ⅱ）中的结论．

    查看答案和解析>>

    科目：高中数学 来源：2013届江苏姜堰市高二第二学期期中理科数学试卷（解析版） 题型：解答题

    已知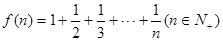．经计算得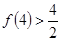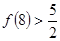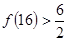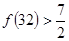，，，，，通过观察，我们可以得到一个一般性的结论．

    （1）试写出这个一般性的结论；

    （2）请用数学归纳法证明这个一般性的结论；

    （3）对任一给定的正整数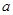，试问是否存在正整数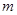，使得？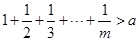

    若存在，请给出符合条件的正整数的一个值；若不存在，请说明理由．

     

    查看答案和解析>>

    同步练习册答案