
分析 (1)求导数,确定切线的斜率,求得切点坐标,进而可求曲线在x=0处的切线方程;
(2)由题意得$\frac{5}{\sqrt{2{x}_{0}+1}}$=$\frac{5}{2}$,求得切点坐标,进而可求曲线上与直线5x-2y+1=0平行的切线的方程.
解答 解:y′=(5$\sqrt{2x+1}$)′=5•$\frac{1}{2}$$(2x+1)^{-\frac{1}{2}}$•(2x+1)′=$\frac{5}{\sqrt{2x+1}}$.
(1)当x=0时导数值为5,所以曲线y=5$\sqrt{2x+1}$在x=0处的切线的斜率为k=5,
又切点坐标为(0,5),所以切线方程为y-5=5x,即5x-y+5=0.
(2)设切点坐标为(x0,y0),则切线斜率为$\frac{5}{\sqrt{2{x}_{0}+1}}$.
由题意得$\frac{5}{\sqrt{2{x}_{0}+1}}$=$\frac{5}{2}$.∴x0=$\frac{3}{2}$,切点坐标为($\frac{3}{2}$,10),
∴切线方程为y-10=$\frac{5}{2}$(x-$\frac{3}{2}$),
即为10x-4y+25=0.
点评 本题考查导数知识的运用,考查导数的几何意义,求出切线的斜率是关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | <b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
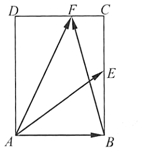 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )| A. | 2-$\sqrt{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对于命题p:?x∈R,使得x2+x+1<0,则¬P:?x∈R,均有x2+x+1≥0 | |
| B. | “x=1”是“x2-4x+3=0”的充分不必要条件 | |
| C. | 命题“若x2-4x+3=0,则x=1”的逆否命题为“若x≠1,则x2-4x+3≠0” | |
| D. | 若p∧q为假命题,则p、q均为假命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com