
|
(Ⅰ)求证:AB1//面BDC1;
(Ⅱ)求二面角C1—BD—C的余弦值;
(Ⅲ)在侧棱AA1上是否存在点P,使得
CP⊥面BDC1?并证明你的结论.
(I)证明:
连接B1C,与BC1相交于O,连接OD
∵BCC1B1是矩形,
∴O是B1C的中点.
|
∴OD//AB1.………………………………………………2分
∵AB1![]() 面BDC1,OD
面BDC1,OD![]() 面BDC1,
面BDC1,
∴AB1//面BDC1.…………………………………………4分
(II)解:如力,建立空间直角坐标系,则
C1(0,0,0),B(0,3,2),C(0,3,0),A(2,3,0),
D(1,3,0)……………………5分
设![]() =(x1,y1,z1)是面BDC1的一个法向量,则
=(x1,y1,z1)是面BDC1的一个法向量,则
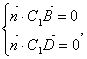
即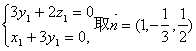 .…………6分
.…………6分
易知![]() =(0,3,0)是面ABC的一个法向量.
=(0,3,0)是面ABC的一个法向量.
 .…………………………8分
.…………………………8分
∴二面角C1—BD—C的余弦值为![]() .………………………………9分
.………………………………9分
(III)假设侧棱AA1上存在一点P(2,y,0)(0≤y≤3),使得CP⊥面BDC1.
则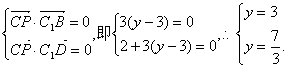
∴方程组无解.
∴假设不成立.
∴侧棱AA1上不存在点P,使CP⊥面BDC1.……………14分


科目:高中数学 来源: 题型:
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=| 2 |
| 2 |
| 2 |
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com