
解法一:由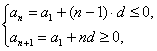
即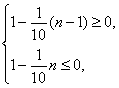
解得10≤n≤11.∴取10或11时Sn取最小值.
解法二:∵S9=S12,∴a10+a11+a12=0.?∴3a11=0.
∴a11=0.∵a1<0,∴前10项或前11项和最小.
解法三:∵S9=S12,∴Sn的图象所在的抛物线的对称轴为x=![]() =10.5.
=10.5.
又a1<0,?∴{an}的前10项或前11项的和最小.
解法四:由S9=S12,得
9a1+![]() d=12a1+
d=12a1+![]() d.
d.
化简得a1=-10d.
∵a1<0,∴d>0.
此时Sn=na1+![]() n(n-1)d=
n(n-1)d=![]() n2+(a1-
n2+(a1-![]() )n?=
)n?=![]() n2-
n2-![]() n.
n.
∵n∈N*且-![]() =
=![]() ,
,
∴当n=10或n=11时Sn最小,即{an}的前10项或前11项的和最小.
点评:在上述四种解法中,解法一、二是利用数列的特殊性来解决问题,解法三、四是利用函数的共性来解决问题,解法四是基本方法,是通性通法.


科目:高中数学 来源:2014届江西省高一下学期第一次月考数学试卷(解析版) 题型:选择题
已知等差数列{an}中,a2=6,a5=15.若bn=a2n,则数列{bn}的前5项和等于( )
(A)30 (B)45 (C)90 (D)186
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com