已知函数f(x)=x2-alnx(a∈R).
(Ⅰ)若a=2,求证:f(x)在(1,+∞)上是增函数;
(Ⅱ)求f(x)在[1,e]上的最小值.
【答案】
分析:(Ⅰ)要证函数在(1,+∞)上是增函数,只需要证明其导数大于0即可;
(Ⅱ)求导函数先研究函数的单调性,确定极值,从而确定函数的最值,分类讨论是解题的关键.
解答:证明:(Ⅰ)当a=2时,f(x)=x
2-2lnx,
当x∈(1,+∞)时,
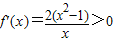
,
所以f(x)在(1,+∞)上是增函数. (5分)
(Ⅱ)解:
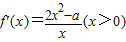
,
当x∈[1,e],2x
2-a∈[2-a,2e
2-a].
若a≤2,则当x∈[1,e]时,f′(x)≥0,
所以f(x)在[1,e]上是增函数,
又f(1)=1,故函数f(x)在[1,e]上的最小值为1.
若a≥2e
2,则当x∈[1,e]时,f′(x)≤0,
所以f(x)在[1,e]上是减函数,
又f(e)=e
2-a,所以f(x)在[1,e]上的最小值为e
2-a.
若2<a<2e
2,则当
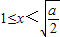
时,f′(x)<0,此时f(x)是减函数;
当
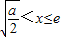
时,f′(x)>0,此时f(x)是增函数.
又
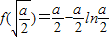
,
所以f(x)在[1,e]上的最小值为
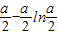
.
综上可知,当a≤2时,f(x)在[1,e]上的最小值为1;
当2<a<2e
2时,f(x)在[1,e]上的最小值为
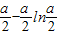
;
当a≥2e
2时,f(x)在[1,e]上的最小值为e
2-a.(13分)
点评:本题以函数为载体,考查函数的单调性与函数的最值.利用导数研究函数的单调性比用函数单调性的定义要方便,但应注意f′(x)>0(或f′(x)<0)仅是f(x)在某个区间上为增函数(或减函数)的充分条件.

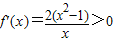 ,
,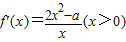 ,
,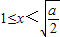 时,f′(x)<0,此时f(x)是减函数;
时,f′(x)<0,此时f(x)是减函数;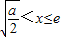 时,f′(x)>0,此时f(x)是增函数.
时,f′(x)>0,此时f(x)是增函数.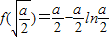 ,
,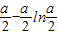 .
.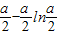 ;
;

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<