
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
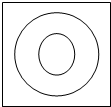 如图,在墙上挂着一块边长为16cm的正方形木板,上面画了大、小两个同心圆,半径分别为2cm,6cm,某人站在3m之外向此板投镖,设投镖击中线上或没有投中木板时都不算(可重投),问:
如图,在墙上挂着一块边长为16cm的正方形木板,上面画了大、小两个同心圆,半径分别为2cm,6cm,某人站在3m之外向此板投镖,设投镖击中线上或没有投中木板时都不算(可重投),问:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”.当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生510天.
原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”.当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生510天.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2\sqrt{2}}{3}$,经过椭圆的左顶点A(-3,0)作斜率为k(k≠0)的直线l交椭圆C于点D,交轴于点E
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2\sqrt{2}}{3}$,经过椭圆的左顶点A(-3,0)作斜率为k(k≠0)的直线l交椭圆C于点D,交轴于点E查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com