Question

已知二次函数f（x）=ax²+bx+c，（a，b，c∈R）满足：对任意实数x，都有f（x）≥x，且当x∈（1，3）时，有成立．
（1）证明：f（2）=2；
（2）若f（-2）=0，f（x）的表达式；
（3）设，x∈[0，+∞），若g（x）图上的点都位于直线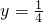的上方，求实数m的取值范围．

Answer 1

解：（1）由条件知f（2）=4a+2b+c≥2恒成立
又∵取x=2时，与恒成立，
∴f（2）=2．
（2）∵
∴4a+c=2b=1，
∴b=，c=1-4a
又f（x）≥x恒成立，即ax²+（b-1）x+c≥0恒成立．
∴，整理得0
故可以解出：，
∴．
（3）解法1：由分析条件知道，只要f（x）图象（在y轴右侧）总在直线上方即可，也就是直线的斜率小于直线与抛物线相切时的斜率位置，
于是：
∴．
解法2：必须恒成立，
即x²+4（1-m）x+2＞0在x∈[0，+∞）恒成立．
①△＜0，即[4（1-m）]²-8＜0，解得：；
②
解出：．又时，经验证不合题意
总之，．
分析：（1）由已知f（2）≥2恒成立，又由成立得（2）≤，由此两种情况可得f（2）=2．
（2）f（-2）=0，由（1）证明知f（2）=2，f（x）的表达式中有三个未知数，由两函数值只能得出两个方程，再对任意实数x，都有f（x）≥x，这一恒成立的关系得到一0，由此可以得到a=，将此三方程联立可解出三个参数的值，求出f（x）的表达式；
（3）方法一：由题f（x）图象（在y轴右侧）总在直线上方即可，也就是直线的斜率小于直线与抛物线相切时的斜率位置，由于f（x）图象与y轴交点在直线与y轴交点上方，在与y轴相交点处的切线斜率为，故在直线与二次函数相切的切点处一定有切线的斜率大于直线的斜率，且＞，将两个方程联立，用判别式为0求m的最大值．
方法二：必须恒成立，即x²+4（1-m）x+2＞0在x∈[0，+∞）恒成立．
转化为二次函数图象与x轴在x∈[0，+∞）无交点的问题，由于g（x）的单调性不确定，故本题要分两种情况讨论，一种是对称轴在y轴右侧，此时需要判别式小于0，一类是判别式大于0，对称轴小于0，且x=0处的函数值大于等于0，转化出相应的不等式求解．
点评：本题是二次函数的一道综合题，考查到了分类讨论的思想，对分析转化的推理能力要求较高．