活动:让学生自主探究题目中给出的条件,本例中给出的实际上是一个图像,它的解析式为y=Asin(ωx+φ)+B(其中A>0,ω>0),这是学生未遇到过的.教师应引导学生思考它与y=Asin(ωx+φ)的图像的关系,它只是把y=Asin(ωx+φ)(其中A>0,ω>0)的图像向上(B>0)或向下(B<0)平移|B|个单位.由图像可知,取最大值与最小值时相应的x的值之差的绝对值只是半个周期.这里φ的确定学生会感到困难,因为题目中毕竟没有直接给出图像,不像例1那样能明显地看出来,应告诉学生一般都会在条件中注明|φ|<π,如不注明,就取离y轴最近的一个即可.
解:由已知条件,知ymax=3,ymin=-5,
则A= (ymax-ymin)=4,B=
(ymax-ymin)=4,B= (ymax+ymin)=-1,
(ymax+ymin)=-1, =
= -
- =
= .
.
∴T=π,得ω=2.
故有y=4sin(2x+φ)-1.
由于点( ,3)在函数的图像上,
,3)在函数的图像上,
故有3=4sin(2× +φ)-1,
+φ)-1,
即sin( +φ)=1.
+φ)=1.
一般要求|φ|< ,故取
,故取 +φ=
+φ= .
.
∴φ= .
.
故所求函数的解析式为y=4sin(2x+ )-1.
)-1.
点拨:这是数形结合的又一典型应用,应让学生明了,题中无图但脑中应有图或根据题意画出草图,结合图像可直接求得A、ω,进而求得初相φ,但要注意初相φ的确定.求初相也是这节课的一个难点.

![]() (ymax-ymin)=4,B=
(ymax-ymin)=4,B=![]() (ymax+ymin)=-1,
(ymax+ymin)=-1,![]() =
=![]() -
-![]() =
=![]() .
.![]() ,3)在函数的图像上,
,3)在函数的图像上,![]() +φ)-1,
+φ)-1,![]() +φ)=1.
+φ)=1.![]() ,故取
,故取![]() +φ=
+φ=![]() .
.![]() .
.![]() )-1.
)-1.

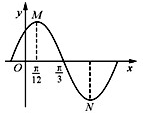 若函数y=Asin(ωx+φ),(A>0,ω>0,|φ|<
若函数y=Asin(ωx+φ),(A>0,ω>0,|φ|< (2012•蚌埠模拟)若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
(2012•蚌埠模拟)若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<