
(Ⅰ)求椭圆C的方程;
(Ⅱ)求直线l斜率的取值范围;
(Ⅲ)是否存在直线l,使得|BP|=|BQ|,若存在,求出l的方程;若不存在,说明理由.
答案:解:圆锥曲线的几何量之间的关系用待定系数法确定方程,利用判别式构建不等式求解参数的方法,利用直线和圆锥曲线的研究方法探究存在性问题.(Ⅰ)
即所求椭圆方程为![]() =1.
=1.
(Ⅱ)点A(5,0)在椭圆的外部,当直线l的斜率不存在时,直线l与椭圆C无交点,所以直线l斜率存在,设直线l的方程为y=k(x-5).
由方程组
得(5k2+4)x2-50k2x+125k2-20=0
依题意△=20(16-80k2)>0,得![]() .
.
(Ⅲ)方法一:利用第二定义探究,设点P、Q到准线的距离分别为dP+dQ.
若存在直线l,使得|BP|=|BQ|
∵![]() =e
=e![]() ,∴dP=dQ,
,∴dP=dQ,
又∵P、Q是椭圆上不同的两点
∴PQ平行于准线.这与PQ过点A矛盾.
∴不存在直线l,使得|BP|=|BQ|.
方法二:利用方程探究,设交点P(x1,y1),Q(x2,y2),PQ的中点为R(x0,y0),则x1+x2=![]() ,
,
x0=![]()
y0=k(x0-5)=k(![]() ,
,
又|BP|=|BQ|![]() BR⊥l
BR⊥l![]() k·kBR=-1
k·kBR=-1
k·kBR= =-1
=-1
![]() 20k2=20k2-4,但0=-4不可能成立,
20k2=20k2-4,但0=-4不可能成立,
所以不存在直线l使得|BP|=|BQ|.


科目:高中数学 来源:2011-2012学年江西省高三第一次统考理科数学 题型:解答题
已知椭圆C: +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径
与以原点为圆心,以椭圆C的短半轴长为半径
的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴
求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点
C( ,0)求实数k的取值范围。
,0)求实数k的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第七次月考理科数学 题型:解答题
已知椭圆C: +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C(
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C( ,0)求实数k的取值范围。
,0)求实数k的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三第一学期第二次阶段考试数学 题型:解答题
已知椭圆C:+=1(a>b>0)的离心率为,且经过点P(1,)。
(1)求椭圆C的方程;
(2)设F是椭圆C的右焦点,M为椭圆上一点,以M为圆心,MF为半径作圆M。问点M满足什么条件时,圆M与y轴有两个交点?
(3)设圆M与y轴交于D、E两点,求点D、E距离的最大值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三元月双周练习数学试卷 题型:解答题
(本小题满分15分)已知椭圆C: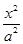 +
+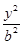 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为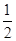 ,且经过点P(1,
,且经过点P(1,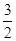 ).
).
(1)求椭圆C的方程;
(2)设F是椭圆C的右焦点,M为椭圆上一点,以M为圆心,MF为半径作圆M.问点M满足什么条件时,圆M与y轴有两个交点? 并求两点间距离的最大值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省高三上学期摸底考试文科数学 题型:解答题
(本题满分14分)已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一
,短轴一
个端点到右焦点的距离为3.
(1)求椭圆C的方程;
(2)过椭圆C上的动点P引圆O: 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com