已知数列{an}的前n项和为Sn,且Sn=2an-2,(n=1,2,3…)数列{bn}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记Sn=a1b1+a2b2+…+anbn,求满足Sn<167的最大正整数n.
解:( I)∵S
n=2a
n-2,∴当n≥2时,a
n=S
n-S
n-1=2a
n-2a
n-1∵a
n≠0,∴
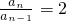
(n≥2),即数列{a
n}是等比数列.
∵S
n=2a
n-2,∴当n=1时,a
1=2,∴
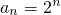
…(3分)
∵点P(b
n,b
n+1)在直线x-y+2=0上
∴b
n-b
n+1+2=0,∴b
n+1-b
n=2
即数列{b
n}是等差数列,又b
1=1,∴b
n=2n-1 …(6分)
( II)S
n=a
1b
1+a
2b
2+…+a
nb
n=1×2+3×2
2+…+(2n-1)×2
n ①(7分)
∴2S
n=1×2
2+3×2
3+…+(2n-1)×2
n+1②
①-②得:-S
n=1×2+2(2
2+2
3+…+2
n)-(2n-1)×2
n+1②…(9分)
∴

(10分)
∵S
n<167,即(2n-3)•2
n+1+6<167
于是(2n-3)•2
n+1<161(11分)
又由于当n=4时,(2n-3)•2
n+1=160
当n=5时,(2n-3)•2
n+1=448(13分)
故满足条件S
n<167最大的正整数n为4(14分)
分析:( I)根据S
n=2a
n-2,当n≥2时,a
n=S
n-S
n-1=2a
n-2a
n-1,可得数列{a
n}是等比数列;利用点P(b
n,b
n+1)在直线x-y+2=0上,可得数列{b
n}是等差数列,故可求数列{a
n}和{b
n}的通项公式;
( II)利用错位相减法求和,利用S
n<167,建立不等式,从而可求满足条件S
n<167最大的正整数.
点评:本题考查数列的通项与求和,考查错位相减法的运用,解题的关键是根据数列通项的特点选择合适的求和方法.

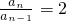 (n≥2),即数列{an}是等比数列.
(n≥2),即数列{an}是等比数列.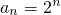 …(3分)
…(3分) (10分)
(10分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案