
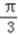 ,则OE=
,则OE=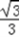 QE=
QE=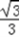 PD.
PD.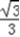 sinθ.
sinθ.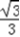 sinθ)×sinθ=sinθcosθ﹣
sinθ)×sinθ=sinθcosθ﹣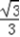 sin2θ,θ∈(0,
sin2θ,θ∈(0,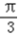 ).
). sin2θ﹣
sin2θ﹣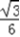 (1﹣cos2θ)=
(1﹣cos2θ)=  sin2θ+
sin2θ+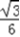 cos2θ﹣
cos2θ﹣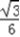 =
= 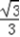 sin(2θ+
sin(2θ+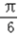 )﹣
)﹣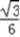 .
.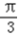 ,所以
,所以 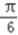 <2θ+
<2θ+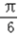 <
< ,
, <sin(2θ+
<sin(2θ+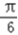 )≤1.所以当2θ+
)≤1.所以当2θ+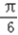 =
= 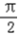 ,即θ=
,即θ= 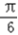 时,S的值最大为
时,S的值最大为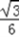 m2.
m2.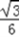 m2,相应θ的值是
m2,相应θ的值是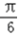 .
.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
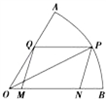
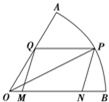 如图,现在要在一块半径为1m.圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设∠BOP=θ.平行四边形MNPQ的面积为S.
如图,现在要在一块半径为1m.圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设∠BOP=θ.平行四边形MNPQ的面积为S.查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三练习数学 题型:解答题
如图,现在要在一块半径为1m.圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设∠BOP=θ,YMNPQ的面积为S.
(1)求S关于θ的函数关系式;
(2)求S的最大值及相应θ的值
1. 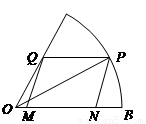
2.
查看答案和解析>>
科目:高中数学 来源:江苏省2013届高一下学期期末考试数学 题型:解答题
如图,现在要在一块半径为1m。圆心角为60°的扇形纸板AOB上剪出一个平行
四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设 的
的
面积为S。
(1)求S关于 的函数关系式;
的函数关系式;
(2)求S的最大值及相应 的值
的值
查看答案和解析>>
科目:高中数学 来源:2010-2011年安徽省高一第二学期期中考试数学试卷 题型:解答题
(12)如图,现在要在一块半径为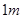 ,圆心角为
,圆心角为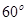 的扇形纸板
的扇形纸板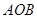 上剪出一个平行四边形
上剪出一个平行四边形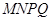 ,使点
,使点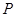 在弧
在弧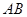 上,点
上,点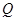 在
在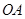 上,点
上,点 ,
, 在
在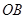 上,设
上,设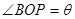 ,
,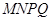 的面积为
的面积为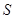 .
.
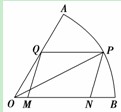
(1)求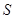 关于
关于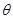 的函数关系式;
的函数关系式;
(2)求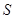 的最大值及相应
的最大值及相应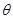 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com