练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知平面α∥β,AB、CD为夹在α、β间的异面线段，E、F分别为AB、CD的中点.求证:EF∥α,EF∥β.

    分析:要证EF∥α，根据线面平行的判定定理，只需在α内找一条直线与EF平行；或过EF作一平面，使该平面与α平行，据面面平行的性质定理即可证得.

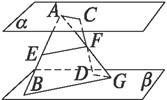
    证法一:

    连结AF并延长交β于G?.

    ∵AG∩CD=F,

    ∴AG、CD确定平面γ，且γ∩α=AC,γ∩β=DG.

    ∵α∥β,∴AC∥DG.∴∠ACF=∠GDF.

    又∠AFC=∠DFG，CF=DF,

    ∴△ACF≌△GDF.∴AF=FG.

    又AE=BE,∴EF∥BG.

    ∵BGβ,∴EF∥β.

    同理,FE∥α.

    证法二:∵AB与CD为异面直线,∴ACD.

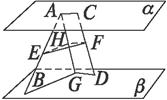
    在A、C、D确定的平面内过点A作AG∥CD交β于点G，取AG的中点H，连结AC、HF.

    ∵α∥β,∴AC∥DG∥FH.

    ∵DGβ,∴HF∥β.

    又∵E为AB的中点,

    ∴EH∥BG.∴EH∥β.

    又EH∩HF=H,∴平面EHF∥β.

    ∵EF平面EHF,∴EF∥β.同理,EF∥α.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•石景山区一模）如图，已知平面α∩β=l，A、B是l上的两个点，C、D在平面β内，且DA⊥α，CB⊥α，AD=4，AB=6，BC=8，在平面α上有一个动点P，使得∠APD=∠BPC，则P-ABCD体积的最大值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线AB与平面α所成角为60°，其中点B∈平面α，点A∉平面α，点P是平面α上的动点，且P到直线AB的距离为2，则|PB|的取值范围为
    [2，
    4
    		3
    3
    ]
    [2，
    4
    		3
    3
    ]
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2004•河西区一模）如图，已知平面α⊥平面β，α∩β=AB，点C∈α，点D∈β，且AB=AC=BC=2
    		3
    ，E为BC的中点，AC⊥BD，BD=6．
    （Ⅰ）求证：BD⊥平面α；
    （Ⅱ）求证：平面AED⊥平面BCD；
    （Ⅲ）求三棱锥C-AED的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知对任意平面向量
    AB
    =(x，y)    ，将
    AB
    绕其起点沿顺时针方向旋转θ角得到向量
    AP
    =(xcosθ+ysinθ，-xsinθ+ycosθ)    ，叫做将点B绕点A沿顺时针方向旋转θ角得到点P．
    （1）已知平面内点A（1，2），点B(1+
    		2
    ，2-2
    		2
    )    ，将点B绕点A沿顺时针方向旋转
    π
    4
    得到点P，求点P的坐标；
    （2）设平面内曲线3x2+3y2+2xy=4上的每一点绕坐标原点O沿顺时针方向旋转
    π
    4
    得到的点的轨迹是曲线C，求曲线C的方程；
    （3）过（2）中曲线C的焦点的直线l与曲线C交于不同的两点A、B，当
    OA
    •
    OB
    =0    时，求△AOB的面积．

    查看答案和解析>>

    同步练习册答案