
圆锥侧面展开图的扇形周长为2a,求该圆锥侧面面积的最大值.
|
分析:要求圆锥侧面面积的最大值,首先需表示出圆锥侧面的面积,为此需要求出圆锥的底面半径和母线长,但已知中给出的是扇形的周长,而扇形的周长由圆锥的母线长与其底面圆的周长组成,因此可建立圆锥的底面半径与母线长的函数关系式. 解:设圆锥的母线长和底面圆的半径分别为l,r. 由题意,得2l+2πr=2a,所以l=a-πr, 则S圆锥侧=πrl=πr(a-πr)=-(πr)2+πra=-π2 故当r= 即当r= 点评:本题是以旋转体为背景的二次函数的最值问题.解决此类问题,首先设变量,其次根据已知条件,建立关于所设变量的函数关系式,最后利用函数的性质求出最值. |


科目:高中数学 来源:2009-2010学年广东省佛山市高明一中高一(上)期末数学试卷(文科)(必修2)(解析版) 题型:解答题
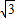 .求:
.求: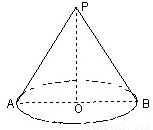
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com