
(Ⅰ)求异面直线AB与MD所成角的大小;
(Ⅱ)求点B到平面OCD的距离.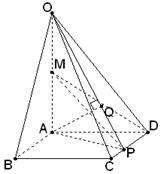
本小题主要考查直线与直线、直线与平面的位置关系、异面直线所成角及点到平面的距离等知识,考查空间想象能力和思维能力,用综合法或向量法解决立体几何问题的能力.
方法一(综合法)
(1)![]()
![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角(或其补角)
所成的角(或其补角)
作![]() 连接
连接![]()
![]()
![]()
![]() ,
,![]()
所以 ![]() 与
与![]() 所成角的大小为
所成角的大小为![]()
(2)![]() 点A和点B到平面OCD的距离相等,
点A和点B到平面OCD的距离相等,
连接OP,过点A作![]() 于点Q,
于点Q,
![]()
![]()
又 ![]() ,线段AQ的长就是点A到平面OCD的距离
,线段AQ的长就是点A到平面OCD的距离
![]() ,
,![]()
 ,所以点B到平面OCD的距离为
,所以点B到平面OCD的距离为![]() .
.

方法二(向量法)
作![]() 于点P,如图,分别以AB,AP,AO所在直线为
于点P,如图,分别以AB,AP,AO所在直线为![]() 轴建立直角坐标系
轴建立直角坐标系
![]() ,
,
(1)设![]() 与
与![]() 所成的角为
所成的角为![]() ,
,
![]()
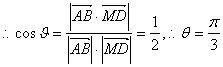 ,
,
![]()
![]() 与
与![]() 所成角的大小为
所成角的大小为![]()
(2) ![]()
![]() 设平面OCD的法向量为
设平面OCD的法向量为![]() ,则
,则![]()
得 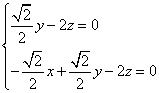
取![]() ,解得
,解得![]()
设点B到平面OCD的距离为![]() ,则
,则![]() 为
为![]() 在向量n上的投影的绝对值,
在向量n上的投影的绝对值,
![]() ,
, 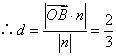 .
.
所以点B到平面OCD的距离为![]()


科目:高中数学 来源: 题型:
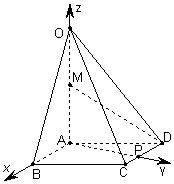
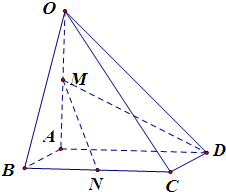 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题查看答案和解析>>
科目:高中数学 来源: 题型:
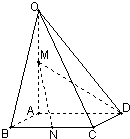 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=| π | 4 |
查看答案和解析>>
科目:高中数学 来源:江苏同步题 题型:解答题
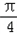 ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.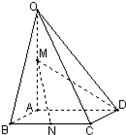
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com