
 ,⊙O的直径AB=2,C是
,⊙O的直径AB=2,C是 的中点,D为AC的中点,
的中点,D为AC的中点,
| 解:(Ⅰ)连接OC,因为OA=OC,D为AC的中点, 所以AC⊥OD, 又PO⊥底面⊙O, AC  底面⊙O, 底面⊙O,所以AC⊥PO, 因为OD,PO是平面POD内的两条相交直线, 所以AC⊥平面POD, 而AC  平面PAC, 平面PAC,所以平面POD⊥平面PAC。 (Ⅱ)在平面POD中,过O作OH⊥PD于H,由(Ⅰ)知,平面POD⊥平面PAC, 所以OH⊥平面PAC, 又PA  平面PAC,所以 平面PAC,所以 , ,在平面PAO中,过O作OG⊥PA于G, 连接HG,则有PA⊥平面OGH,从而PA⊥HG, 所以∠OGH是二面角B-PA-C的平面角, 在Rt△ODA中,  , ,在Rt△POD中,  , ,在Rt△POA中,  , ,在Rt△OHG中,  , ,所以  , ,故二面角B-PA-C的余弦值为  。 。 |
 |


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
 如图,在圆锥PO中,已知PO=
如图,在圆锥PO中,已知PO=| 2 |
 |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
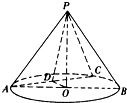 如图,在圆锥PO中,已知PO=
如图,在圆锥PO中,已知PO=| 2 |
 |
| AB |
查看答案和解析>>
科目:高中数学 来源:四川省期末题 题型:解答题
 ,⊙OD的直径AB=2,点C在
,⊙OD的直径AB=2,点C在 上,且∠CAB=30°,D为AC的中点.
上,且∠CAB=30°,D为AC的中点.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏州市张家港外国语学校高二(上)周日数学试卷5(理科)(解析版) 题型:解答题
 如图,在圆锥PO中,已知PO=
如图,在圆锥PO中,已知PO= ,⊙O的直径AB=2,C是
,⊙O的直径AB=2,C是 的中点,D为AC的中点.
的中点,D为AC的中点.查看答案和解析>>
科目:高中数学 来源:2011年湖南省高考数学试卷(文科)(解析版) 题型:解答题
 如图,在圆锥PO中,已知PO=
如图,在圆锥PO中,已知PO= ,⊙OD的直径AB=2,点C在
,⊙OD的直径AB=2,点C在 上,且∠CAB=30°,D为AC的中点.
上,且∠CAB=30°,D为AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com