
 =(sinα,cosα),
=(sinα,cosα), =(cos2α,sin2α),且
=(cos2α,sin2α),且
 ,求向量
,求向量 与
与 的夹角的余弦值.
的夹角的余弦值. 、
、 互相垂直,得
互相垂直,得 =sin3α=0,结合α为锐角,得3α=π,可得α=
=sin3α=0,结合α为锐角,得3α=π,可得α= ;
; 、
、 的模均为1,可得
的模均为1,可得 =(2
=(2 +2
+2 )(2
)(2 +2
+2 )=8
)=8 ,再计算出向量
,再计算出向量 与
与 的模都等于4,结合两个向量的夹角公式即可算出
的模都等于4,结合两个向量的夹角公式即可算出 与
与 的夹角的余弦值.
的夹角的余弦值. ,
, =(sinα,cosα),
=(sinα,cosα), =(cos2α,sin2α),
=(cos2α,sin2α), =sinαcos2α+cosαsin2α=0,即sin3α=0
=sinαcos2α+cosαsin2α=0,即sin3α=0 )
)
 ,得
,得 =(sinα,cosα)=(
=(sinα,cosα)=( ,
, ),
), =(cos2α,sin2α)=(-
=(cos2α,sin2α)=(- ,
, ),
), |=|
|=| |=1,且
|=1,且 =0
=0 =(2
=(2 +2
+2 )(2
)(2 +2
+2 )
)
 +16
+16 +4
+4
 =8
=8
 |=
|= =4,|
=4,| |=
|= =4
=4 与
与 的夹角为θ,可得cosθ=
的夹角为θ,可得cosθ= =
= =
=
 与
与 的夹角的余弦值为
的夹角的余弦值为 .
.

科目:高中数学 来源: 题型:
| a |
| b |
| c |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| b |
| ||
| 2 |
| a |
| c |
| ||
| 4 |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| x |
| 2 |
| n |
| x |
| 2 |
| m |
| n |
| 3 |
| 5 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:四川省古蔺县中学校2012届高三第一学月能力监测数学试题 题型:044
已知A为锐角,向量![]() =(sinA,cosA),
=(sinA,cosA),![]() =(
=(![]() ,-1),且
,-1),且![]() ·
·![]() =1.
=1.
(Ⅰ)求角A的大小;
(Ⅱ)求函数f(x)=cos2x+4cosAsinx(x∈R)的值域.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| a |
| b |
| c |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| b |
| ||
| 2 |
| a |
| c |
| ||
| 4 |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源:《3.1 两角和与差的正弦、余弦和正切公式》2011年同步练习(人教A版:必修4)(解析版) 题型:解答题
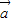 =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),
=(cosβ,sinβ), =(
=( ,-
,- ).
).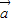 •
• =
= ,
, •
•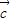 =
=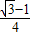 ,求角2β-α的值;
,求角2β-α的值;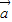 =
= +
+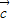 ,求tanα的值.
,求tanα的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com