练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    网等差数列{an}的前n项和为Sn，若a2＋a8＋a11＝30，那么S13值的是

    [　　]
    A．

    130

    B．

    65

    C．

    70

    D．

    以上都不对

    答案：A
    解析：


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)（n∈N）    顺次为一次函数图象上高考资源网的点，   点列A1(x1,0)、A2(x2,0)、…、An(xn,0)（n∈N）    顺次为x轴正半轴上高考资源网的点，其中x1=a（0＜a＜1），    对于任意n∈N，点An、Bn、An+1构成以

        Bn为顶点的等腰三角形。

    ⑴求{yn}的通项公式，且证明{yn}是等差数列；

    ⑵试判断xn+2-xn是否为同一常数（不必证明），并求出数列{xn}的通项公式；

    ⑶在上高考资源网述等腰三角形AnBnAn+1中，是否存在直角三角形？若有，求出此时a值；

    若不存在， 请说明理由。

    查看答案和解析>>

    科目：高中数学 来源：河北省衡水中学2010届高三第三次模拟考试数学试卷（文科） 题型：解答题

    (本小题满分12分高☆考♂资♀源?网)
    已知等差数列{an}的首项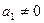，前n项和为Sn，且S4+a2=2S3；等比数列{bn}满足b1=a2，b2=a4
    （1）若a1=2，设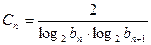，求数列{cn}的前n项的和Tn；
    （2）在（1）的条件下，若有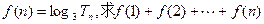的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知是业义在R上的不恒为零的函数，且对于任意实数网满足： ，考察下列结论：①②数列{an}为等比例数列；③数列{bn}为等差数列。

    其中正确的结论是（    ）

    A．①②③    B．①③ C．①② D．②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知是业义在R上的不恒为零的函数，且对于任意实数网满足： ，考察下列结论：①②数列{an}为等比例数列；③数列{bn}为等差数列。

    其中正确的结论是（    ）

    A．①②③    B．①③ C．①② D．②③

    查看答案和解析>>

    同步练习册答案