

 ,△CAD为直角三角形,∠CAD=
,△CAD为直角三角形,∠CAD= ,由∠CAB=∠CAD+∠DAB,知 tan∠CAB=-
,由∠CAB=∠CAD+∠DAB,知 tan∠CAB=- ,设E在角平分线上,则∠CAE=
,设E在角平分线上,则∠CAE= ∠CAB,设tan∠CAE=k,则-
∠CAB,设tan∠CAE=k,则- =
= ,由此能求出该单位向量.
,由此能求出该单位向量. ,②△CAD为直角三角形
,②△CAD为直角三角形 ,
, +arctan
+arctan
 ,
, ∠CAB,
∠CAB, =
= ,
,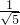 =
= ,(负值解不合所设,舍去)
,(负值解不合所设,舍去) ,
, ).
). ,
, ).
).

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com