
已知圆![]() 为ΔABC的内切园,且BC中点为(1,-1),BC∥x轴。⑴求ΔABC顶点A的轨迹方程。⑵求|BC|的范围。⑶试问ΔABC的面积是否存在最小值?请证明你的判断。
为ΔABC的内切园,且BC中点为(1,-1),BC∥x轴。⑴求ΔABC顶点A的轨迹方程。⑵求|BC|的范围。⑶试问ΔABC的面积是否存在最小值?请证明你的判断。
(Ⅰ) x+y=1(x<0) (Ⅱ) (![]() ,+∞) (Ⅲ)
,+∞) (Ⅲ)![]() 有最小值
有最小值![]()
⑴设A(m,n),过A的园的切线y-n=k(x-m) 即kx-y+n-km=0
则![]() ,即(m2-1)k2-2mnk+n2-1=0 Δ>0得m2+n2>1 ①
,即(m2-1)k2-2mnk+n2-1=0 Δ>0得m2+n2>1 ①
设此方程两解k1=kAB k2=kAC 则![]() ②
②
另一方面BC:y=-1 由AB:y-n=k1(x-m) AC:y-n=k2(x-m)
解得:![]()
由于BC中点为(1,-1),∴![]()
即![]() ,把②代入得:
,把②代入得:![]()
即:得m+n=1 由①及⊙O为ΔABC内切园知,A的轨迹方程为x+y=1(x<0) (6分)
⑵由⑴知n>1,m<0 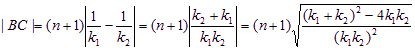
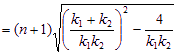 (8分)
(8分)
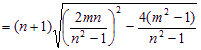
![]()
![]() ∴BC的范围为(
∴BC的范围为(![]() ,+∞) (10分)
,+∞) (10分)
⑶存在 易知![]()
![]() ,令t=n-1>0 n=t+1
,令t=n-1>0 n=t+1
![]()
![]() (12分)
(12分)
证法1:再令![]() ,则
,则![]()
![]() 上增函数。
上增函数。
易知![]() ∴
∴![]() 内恰有一解,设此解为x0,即
内恰有一解,设此解为x0,即![]() 由
由![]() 是增函数,则
是增函数,则![]() 为减函数。
为减函数。
![]() 是增函数。
是增函数。
![]() 存在最小值
存在最小值![]() ,即ΔABC面积有最小值。 (14分)
,即ΔABC面积有最小值。 (14分)
证法2: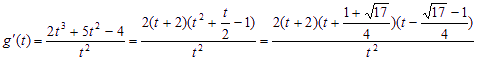
易知![]() 为减函数。
为减函数。![]() 为增函数
为增函数
![]() 有最小值
有最小值![]() ,∴ΔABC面积有最小值
,∴ΔABC面积有最小值


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
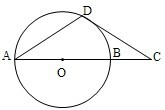 本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
|
|
| ab |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北武汉部分重点中学高二上期中文科数学试卷(带解析) 题型:解答题
本小题满分13分)
已知圆 ,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点.
,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点.
(Ⅰ)若△ABC的重心是G( ,2),求BC中点D的坐标及直线BC的方程;
,2),求BC中点D的坐标及直线BC的方程;
(Ⅱ)若直线AB与直线AC的倾斜角互补,求证:直线BC的斜率为定值.
查看答案和解析>>
科目:高中数学 来源:2014届湖北武汉部分重点中学高二上期中文科数学试卷(解析版) 题型:解答题
本小题满分13分)
已知圆 ,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点.
,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点.
(Ⅰ)若△ABC的重心是G( ,2),求BC中点D的坐标及直线BC的方程;
,2),求BC中点D的坐标及直线BC的方程;
(Ⅱ)若直线AB与直线AC的倾斜角互补,求证:直线BC的斜率为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com