
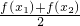 >f(
>f( )
) <0故可借助函数的图象的单调性得出结论
<0故可借助函数的图象的单调性得出结论 ,可借助函数图象上点的几何意义得出结论
,可借助函数图象上点的几何意义得出结论 ,故可借助函数的图象上点的切线斜率变化规律得出结论
,故可借助函数的图象上点的切线斜率变化规律得出结论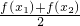 >f(
>f( )说明函数是一个凹函数,以此由函数图象即可得出结论.
)说明函数是一个凹函数,以此由函数图象即可得出结论. (1)∵f(x)=2x-1为R上的单调增函数,故满足0<x1<x2的任意x1,x2,总有f(x1)<f(x2),即f(x2)-f(x1)>0,∴(x2-x1)[f(x2)-f(x1)]>0,故(1)错误;
(1)∵f(x)=2x-1为R上的单调增函数,故满足0<x1<x2的任意x1,x2,总有f(x1)<f(x2),即f(x2)-f(x1)>0,∴(x2-x1)[f(x2)-f(x1)]>0,故(1)错误; =
= =
= ,其几何意义为f(x)图象上的点与原点连线斜率,由函数f(x)=2x-1在(0,+∞)上的图象可知y=
,其几何意义为f(x)图象上的点与原点连线斜率,由函数f(x)=2x-1在(0,+∞)上的图象可知y= 为增函数,∵0<x1<x2,
为增函数,∵0<x1<x2, <
< ,即x2f(x1)<x1f(x2),(2)正确;
,即x2f(x1)<x1f(x2),(2)正确; ?函数f(x)在所给的区间上导数值恒大于1,∴(3)错误;
?函数f(x)在所给的区间上导数值恒大于1,∴(3)错误;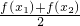 >f(
>f( )反映函数f(x)为凹函数,由f(x)=2x-1的图象可知此函数在(0,+∞)上确为凹函数,(4)正确
)反映函数f(x)为凹函数,由f(x)=2x-1的图象可知此函数在(0,+∞)上确为凹函数,(4)正确

科目:高中数学 来源: 题型:
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com