分析:(1)欲证A
1B⊥平面CDE,只需证明A
1B垂直平面CDE内两条相交直线即可,而A
1B⊥DE,CD⊥A
1B,CD∩DE=D,CD,DE?面CDE,满足线面垂直的判定定理,结论得证;
(2)根据CF为A
1C在面CDE上的射影,则∠A
1CF是A
1C和面CDE所成的角,在Rt△A
1FC中求出此角即可;
(3)在Rt△CDE中,求出CD,DE的长,以及
S△CDE=,最后根据三棱锥的体积公式进行求解即可.
解答:解:(1)∵AA
1⊥底面ABC,CD?面ABC
∴AA
1⊥CD
∵AC=BC,点D是AB的中点
∴AB⊥CD
∵AA
1∩AB=A,AA
1,AB?面A
1ABB
1∴CD⊥面A
1ABB
1∵A
1B?面A
1ABB
1∴CD⊥A
1B
∵正方形A
1ABB
1中,DE∥AB
1,A
1B⊥AB
1∴A
1B⊥DE
∵CD∩DE=D,CD,DE?面CDE
∴A
1B⊥面CDE
(2)设AB
1∩DE=F,
∵A
1B⊥面CDE∴CF为A
1C在面CDE上的射影
∴∠A
1CF是A
1C和面CDE所成的角
在Rt△A
1FC中,A
1F=3,A
1C=
2,∴
sin∠A1CF==,
∴∠A
1CF=60°,∴A
1C和面CDE所成的角为60°
(3)在Rt△CDE中,CD=
,DE=2,∴
S△CDE=∴
VA1-CDE=×S△CDE×A1F= 点评:本题主要考查了线面垂直的判定定理以及线面所成角的度量和体积的计算,同时考查了计算能力和论证推理能力,属于中档题.

 在三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=2
在三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=2

 名校课堂系列答案
名校课堂系列答案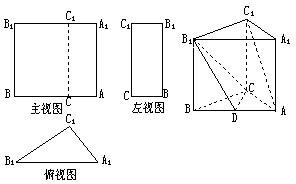 已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,cos∠A1=
已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,cos∠A1= 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.