练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19.设二次函数方程的两根和满足

    (Ⅰ)求实数a的取值范围;

    (Ⅱ)试比较的大小，并说明理由.

    本小题主要考查二次函数、二次方程的基本性质及二次不等式的解法，考查推理和运算能力.

    解法1：(Ⅰ)令g(x)=f(x)-x=x2+(a-1)x+a,则由题意可得

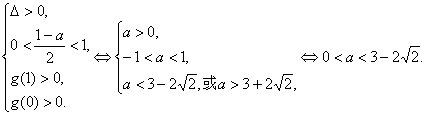
    故所求实数a的取值范围是(0，3-2).

    (Ⅱ)f(0)·f(1)-f(0)=g(0)g(1)=2a2, 令h(a)=2a2.

    ∵当a＞0时h(a)单调增加，

    ∴当0＜a＜3-2时

    0＜h(a)＜h(3-2)=2(3-2)2=2(17-12)

    =2·

    解法2：(Ⅰ)同解法1.

    (Ⅱ)∵f(0)f(1)-f(0)=g(0)g(1)=2a2,由(Ⅰ)知0＜a＜3-2

    ∴4a-1＜12-17＜0,又4a+1＞0,于是

    2a2-=

    即2a2-故f(0)f(1)-f(0)＜

    解法3：(Ⅰ)方程f(x)-x=0x2+(a-1)x+a=0,由韦达定理得

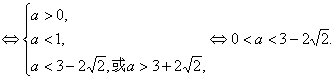
    故所求实数a的取值范围是(0，3-2)

    (Ⅱ)依题意可设g(x)=(x-x1)(x-x2),则由0＜x1＜x2＜1得

    f(0)f(1)-f(0)=g(0)g(1)=x1x2(1-x1)(1-x2)=［x1(1-x1)］［x2(1-x2)］

    ＜

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【解析图片】设二次函数f（x）=ax2+bx+c（a，b，c∈R）满足f（-1）=0，且对任意实数x，均有x-1≤f（x）≤x2-3x+3恒成立．
    （1）求f（x）的表达式；
    （2）若关于x的不等式f（x）≤nx-1的解集非空，求实数n的取值的集合A．
    （3）若关于x的方程f（x）=nx-1的两根为x1，x2，试问：是否存在实数m，使得不等式m2+tm+1≤|x1-x2|对任意n∈A及t∈[-3，3]恒成立？若存在，求出m的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设二次函数f（x）=-x2+ax+a，方程f（x）-x=0的两根x1和x2满足0＜x1＜x2＜1．
    （Ⅰ）求实数a的取值范围；
    （Ⅱ）试比较f（0）•f（1）-f（0）与
    115
    的大小，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数f（x）=ax2+bx+1（a，b∈R，a＞0），设方程f（x）=x的两个实数根为x1和x2．
    （1）如果x1＜2＜x2＜4，设二次函数f（x）的对称轴为x=x0，求证：x0＞-1；
    （2）如果|x1|＜2，|x2-x1|=2，求b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设二次函数方程的两根和满足

      （Ⅰ）求实数a的取值范围;

      （Ⅱ）试比较的大小，并说明理由.

    查看答案和解析>>

    同步练习册答案