练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    二次函数f(x)＝ax2＋bx＋c(x∈R)的部分对应值如下表：

    不求a、b、c的值，可以判断，方程ax2＋bx＋c＝0的两个根所在的区间是

    [　　]

    A．(－3，－1)和(2，4)

    B．(－3，－1)和(－1，1)

    C．(－1，1)和(1，2)

    D．(－∞，－3)和(－∞，3)

    答案：A
    解析：

    　　由根的存在性原则，若m、n为实数，且m＜n，函数f(x)满足f(m)·f(n)＜0，则必存在x0∈(m，n)，使得f(x0)＝0．

    　　因为f(－3)＝6，f(－1)＝－4，于是f(－3)·f(－1)＜0，故必存在x0∈(－3，－1)，f(x0)＝0，即二次方程ax2＋bx＋c＝0在区间(－3，－1)上有一个根．

    　　同理可知，方程在区间(2，4)上也有一个根．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2001～2002学年度 第一学期 教学目标检测 高三数学 题型：022

    二次函数f(x)＝a(x－)(x－)(a＜0)的最大值是________．

    查看答案和解析>>

    科目：高中数学 来源：高三数学教学与测试 题型：044

    已知二次函数f(x)＝a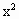＋bx(a，b是常数且a≠0)满足条件：f(2)＝0且方程f(x)＝x有等根．(1)求f(x)的解析式；(2)问是否存在实数m，n(m＜n)，使f(x)的定义域和值域分别为[m，n]和[2m，2n]，如存在，求出m，n的值；如不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：黄冈新内参·高考（专题）模拟测试卷·数学 题型：044

    已知二次函数f(x)＝a＋bx＋c

    (1)若a＞b＞c，且f(1)＝0，证明f(x)的图象与x轴有2个交点；

    (2)在(1)的条件下，是否存在m∈R，使当f(m)＝－a成立时，f(m＋3)为正数，若存在，证明你的结论；若不存在，说明理由．

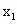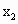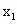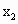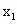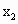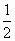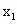    (3)若对、∈R．且＜，f()≠f()，方程f(x)＝[f()＋f(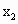)]有2个不等实根，证明必须有一实根属于(、)．

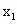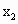    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　人教课标高二版(A选修2―1)　2009－2010学年　第15期　总第171期 人教课标版(A选修2―1) 题型：044

    (1)写出下列命题的否定，并判断其真假：

    p：y＝tanx是奇函数；

    q：＝―2．

    (2)用符号“”与“”表示含有量词的命题“p：已知二次函数f(x)＝a(x2＋1)＋b(x＋1)，则存在实数a，b，使不等式x≤f(x)≤(x2＋1)对任意实数x恒成立”．

    查看答案和解析>>

    科目：高中数学 来源：2007年江苏省如东高级中学高三数学 题型：044

    已知二次函数f(x)＝a(x2－1)＋bx在x∈[－1、1]的最大值为m，最小值为n，且

    (1)、求证：＜2

    (2)、若m＝2，n＝－且a＞0，求a、b

    查看答案和解析>>

    同步练习册答案