
 18、如图,PA是⊙O的切线,切点为A,PCB是⊙O的割线,交⊙O于C、B两点,半径OD⊥BC,垂足为E,AD交PB于点F,BF=PF.
18、如图,PA是⊙O的切线,切点为A,PCB是⊙O的割线,交⊙O于C、B两点,半径OD⊥BC,垂足为E,AD交PB于点F,BF=PF.

科目:高中数学 来源: 题型:
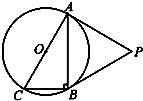 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 A.(不等式选讲选做题)函数y=|x+1|+|x-1|的最小值是
A.(不等式选讲选做题)函数y=|x+1|+|x-1|的最小值是查看答案和解析>>
科目:高中数学 来源:2013届吉林长春市高二第二次月考文科数学试卷(解析版) 题型:解答题
已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F, BP的延长线交AC于点E.
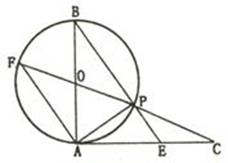
⑴求证:FA∥BE;
⑵求证: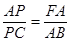
【解析】本试题主要是考查了平面几何中圆与三角形的综合运用。
(1)要证明线线平行,主要是通过证明线线平行的判定定理得到
(2)利用三角形△APC∽△FAC相似,来得到线段成比列的结论。
证明:(1)在⊙O中,∵直径AB与FP交于点O ∴OA=OF
∴∠OAF=∠F ∵∠B=∠F ∴∠OAF=∠B ∴FA∥BE
(2)∵AC为⊙O的切线,PA是弦 ∴∠PAC=∠F
∵∠C=∠C ∴△APC∽△FAC ∴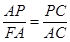
∴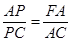 ∵AB=AC
∴
∵AB=AC
∴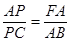
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com