
如图所示,己知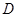 为
为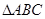 的
的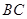 边上一点,
边上一点,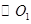 经过点
经过点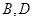 ,交
,交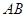 于另一点
于另一点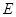 ,
,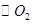 经过点
经过点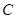 ,
,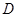 ,交
,交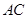 于另一点
于另一点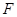 ,
,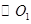 与
与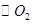 的另一交点为
的另一交点为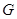 .
.
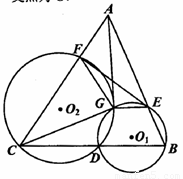
(I)求证: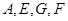 四点共圆;
四点共圆;
(II)若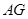 切
切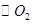 于
于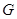 ,求证:
,求证: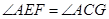 .
.
科目:高中数学 来源: 题型:
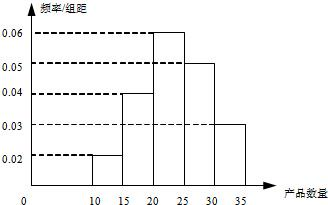 为了调查某厂2000名工人生产某种产品的能力,随机抽查了m位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.已知生产的产品数量在[20,25)之间的工人有6位.
为了调查某厂2000名工人生产某种产品的能力,随机抽查了m位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.已知生产的产品数量在[20,25)之间的工人有6位.查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
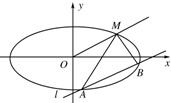 如图所示,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的3倍且经过点M(3,1).平行于OM的直线l在y轴上的截距为m(m≠0),且交椭圆于A,B两不同点.
如图所示,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的3倍且经过点M(3,1).平行于OM的直线l在y轴上的截距为m(m≠0),且交椭圆于A,B两不同点.查看答案和解析>>
科目:高中数学 来源:2013-2014学年云南省昆明市高三上学期第一次摸底调研测试文科数学试卷(解析版) 题型:解答题
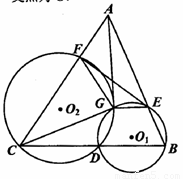
如图所示,己知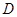 为
为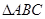 的
的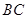 边上一点,
边上一点,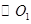 经过点
经过点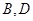 ,交
,交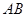 于另一点
于另一点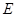 ,
,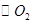 经过点
经过点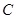 ,
,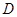 ,交
,交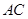 于另一点
于另一点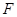 ,
,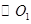 与
与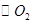 的另一交点为
的另一交点为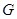 .
.
(I)求证: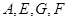 四点共圆;
四点共圆;
(II)若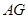 切
切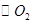 于
于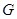 ,求证:
,求证: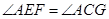 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com