
| CD | 4 |
| FH |
| 3 |
| 2 |
| BD1 |
 解:以D为坐标原点,建立如图所示的空间直角坐标系D-xyz.
解:以D为坐标原点,建立如图所示的空间直角坐标系D-xyz.| 7 |
| 2 |
| FH |
(0-2)2+(
|
| 5 |
| 2 |
| 5 |
| 2 |
| FH |
| 3 |
| 2 |
| BD1 |
| FH |
(-2)2+(
|
| 5 |
| 2 |
| BD1 |
| (-4)2+(-4)2+42 |
| 3 |
| FH |
| BD1 |
| 3 |
| 2 |
| FH |
| BD1 |
| 2 | ||||
|
| ||
| 15 |
| ||
| 15 |


科目:高中数学 来源: 题型:
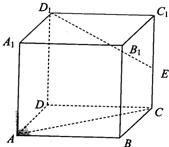 如图所示,在棱长为4的正方体ABCD-A1B1C1D1中,点E是棱CC1的中点.
如图所示,在棱长为4的正方体ABCD-A1B1C1D1中,点E是棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
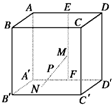 如图,在棱长为4的正方体ABCD-A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )
如图,在棱长为4的正方体ABCD-A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )查看答案和解析>>
科目:高中数学 来源:2014届四川省高二上学期期中考试数学试卷(解析版) 题型:选择题
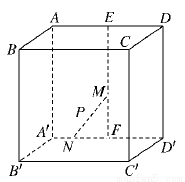
(文)如图,在棱长为4的正方体ABCD—A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′?上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )
A. B. C. D.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江高三上期末考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)如图所示,在棱长为4的正方体ABCD—A1B1C1D1中,点E是棱CC1的中点。

(I)求三棱锥D1—ACE的体积;
(II)求异面直线D1E与AC所成角的余弦值;
(III)求二面角A—D1E—C的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com