解:(I)存在x
1、x
2∈[0,2],使得g(x
1)-g(x
2)≥M成立等价于g(x)
max-g(x)
min≥M
∵g(x)=x
3-x
2-3,∴

∴g(x)在(0,

)上单调递减,在(

,2)上单调递增
∴g(x)
min=g(

)=-
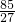
,g(x)
max=g(2)=1
∴g(x)
max-g(x)
min=
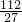
∴满足的最大整数M为4;
(II)对于任意的s、t∈[

,2],都有f(s)≥g(t)成立等价于f(x)≥g(x)
max.
由(I)知,在[

,2]上,g(x)
max=g(2)=1
∴在[

,2]上,f(x)=

+xlnx≥1恒成立,等价于a≥x-x
2lnx恒成立
记h(x)=x-x
2lnx,则h′(x)=1-2xlnx-x且h′(1)=0
∴当
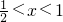
时,h′(x)>0;当1<x<2时,h′(x)<0
∴函数h(x)在(

,1)上单调递增,在(1,2)上单调递减,
∴h(x)
max=h(1)=1
∴a≥1
分析:(I)存在x
1、x
2∈[0,2],使得g(x
1)-g(x
2)≥M成立等价于g(x)
max-g(x)
min≥M;
(II)对于任意的s、t∈[

,2],都有f(s)≥g(t)成立等价于f(x)≥g(x)
max,进一步利用分离参数法,即可求得实数a的取值范围.
点评:本题考查导数在研究函数问题中的应用、由不等式恒成立求解参数范围,考查等价转化思想,这种常规的数学思想方法值得研究.

 +xlnx,g(x)=x3-x2-3.
+xlnx,g(x)=x3-x2-3. ,2],都有f(s)≥g(t)成立,求实数a的取值范围..
,2],都有f(s)≥g(t)成立,求实数a的取值范围..
 )上单调递减,在(
)上单调递减,在( ,2)上单调递增
,2)上单调递增 )=-
)=-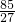 ,g(x)max=g(2)=1
,g(x)max=g(2)=1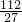
 ,2],都有f(s)≥g(t)成立等价于f(x)≥g(x)max.
,2],都有f(s)≥g(t)成立等价于f(x)≥g(x)max. ,2]上,g(x)max=g(2)=1
,2]上,g(x)max=g(2)=1 ,2]上,f(x)=
,2]上,f(x)= +xlnx≥1恒成立,等价于a≥x-x2lnx恒成立
+xlnx≥1恒成立,等价于a≥x-x2lnx恒成立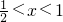 时,h′(x)>0;当1<x<2时,h′(x)<0
时,h′(x)>0;当1<x<2时,h′(x)<0 ,1)上单调递增,在(1,2)上单调递减,
,1)上单调递增,在(1,2)上单调递减, ,2],都有f(s)≥g(t)成立等价于f(x)≥g(x)max,进一步利用分离参数法,即可求得实数a的取值范围.
,2],都有f(s)≥g(t)成立等价于f(x)≥g(x)max,进一步利用分离参数法,即可求得实数a的取值范围.
