解:(Ⅰ)由于
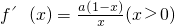
,…(2分)
①当a>0时,易知,当0<x<1时,f'(x)>0,当x>1时,f'(x)<0;
所以f(x)的单调递增区间为(0,1),递减区间为(1,+∞);…(4分)
②当a<0时,同理可知f(x)的单调递减区间为(0,1),递增区间为(1,+∞);…(6分)
(Ⅱ)要证

成立;
只须证

(n≥2,n∈N
*,)
即证lnn<n-1(n≥2,n∈N
*,)
下面证明此式.
证明:令a=1此时f(x)=lnx-x-3,所以f(1)=-4,
由(I)知f(x)=lnx-x-3在(1,+∞)上单调递减,
∴当x∈[1,+∞)时f(x)<f(1),即lnx-x+1<0,
∴lnx<x-1对一切x∈(1,+∞)成立,(12分)
∵n≥2,n∈N
*,则有0<lnn<n-1,
故结论成立.
分析:(I)利用导数求函数的单调区间的步骤是①求导函数f′(x);②解f′(x)>0(或<0);③得到函数的增区间(或减区间),在求单调区间时要注意函数的定义域以及对参数a的讨论情况;
(II)判断lnx<x-1对一切x∈(1,+∞)成立,进而可得证

(n≥2,n∈N
*),即可证得结论.
点评:本题考查利用函数的导数来求函数的单调区间,考查函数单调性的性质,构造函数求解证明不等式问题,属于难题.

 .
.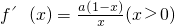 ,…(2分)
,…(2分) 成立;
成立; (n≥2,n∈N*,)
(n≥2,n∈N*,) (n≥2,n∈N*),即可证得结论.
(n≥2,n∈N*),即可证得结论.

 阅读快车系列答案
阅读快车系列答案