练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若(x＋2)n＝xn＋…＋ax3＋bx2＋cx＋2n(n∈N，n≥3)且a∶b＝3∶2，则n＝________．

    答案：11
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2012年普通高等学校招生全国统一考试上海卷理科数学 题型：044

    对于数集X＝{－1，x1，x2，…，xn}，其中0＜x1＜x2＜…＜xn，n≥2，定义向量集Y＝＝{|＝(s，t)，s∈X，t∈X}，若对任意∈Y，存在∈Y，使得·＝0，则称X具有性质P．例如{－1，1，2}具有性质P．

    (1)若x＞2，且{－1，1，2，x}具有性质P，求x的值；

    (2)若X具有性质P，求证：1∈X，且当xn＞1时，x1＝1；

    (3)若X具有性质P，且x1＝1、x2＝q(q为常数)，求有穷数列x1，x2，…，xn的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=x2－4，设曲线y＝f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1,0）（n），其中为正实数.  

     （Ⅰ）用表示xn+1；

    （Ⅱ）若a1=4，记an=lg，证明数列｛｝成等比数列，并求数列｛xn｝的通项公式；

    （Ⅲ）若x1＝4，bn＝xn－2，Tn是数列｛bn｝的前n项和，证明Tn<3.

    查看答案和解析>>

    科目：高中数学 来源：2010年广东省高考冲刺强化训练试卷三文科数学 题型：解答题

    （本小题满分14分）已知函数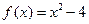，设曲线y＝f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1,0）（n ÎN *），x1＝4．
    （Ⅰ）用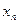表示xn+1；
    （Ⅱ）记an=lg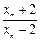，证明数列｛an｝成等比数列，并求数列｛xn｝的通项公式；
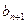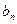    （Ⅲ）若bn＝xn－2，试比较与的大小．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年湖北省、钟祥一中高三第二次联考数学理卷 题型：解答题

    （14分）设函数f(x)＝xn（n≥2，n∈N*）

        （1）若Fn(x)＝f(x－a)＋f(b－x)（0＜a＜x＜b），求Fn(x)的取值范围；

        （2）若Fn(x)＝f(x－b)－f(x－a)，对任意n≥a (2≥a＞b＞0)，

    证明：F(n)≥n(a－b)(n－b)n-2。

     

    查看答案和解析>>

    同步练习册答案