
建一栋新房,门窗需要两种不同尺寸的玻璃,其中大号玻璃40块,小号玻璃100块.已知商店出售甲、乙两种型号的玻璃,每种不同型号的玻璃可同时割得的大、小号尺寸的玻璃数如下表:
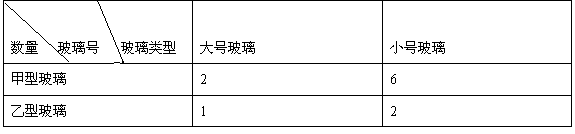
已知甲型玻璃每块40元,乙型玻璃每块16元,问每种玻璃各买多少块可使购买玻璃所用的资金最少?并求出这资金数.
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
某富裕了的农民建一栋新房,门窗需要两种不同尺寸的玻璃,其中大号玻璃40块,小号玻璃100块.已知商店出售甲、乙两种型的玻璃,每种不同型号的玻璃可同时割得大、小号尺寸的玻璃数如下表:

已知甲型玻璃每张40元,乙型玻璃每张16元,问这位农民每种玻璃各买多少张可使购买玻璃所用的资金最少?并求出这资金数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com