
分析 首先,圆x2+y2=4的圆心为原点,半径为2,然后讨论:当过点(2,2)的直线斜率不存在时,方程是x=2,通过验证圆心到直线的距离,得到x=2符合题意;当过点(2,2)的直线斜率存在时,设直线方程为y-2=k(x-2),根据圆心到直线的距离等于半径1,建立关于k的方程,解之得k,进而得到直线的方程.最后综合可得答案.
解答 解:圆x2+y2=4的圆心为原点,半径为2
(1)当过点(2,2)的直线垂直于x轴时,
此时直线斜率不存在,方程是x=2,
因为圆心O(0,0)到直线的距离为d=2=r,所以直线x=2符合题意;
(2)当过点(2,2)的直线不垂直于x轴时,设直线方程为y-2=k(x-2)
即kx-y-2k+2=0
∵直线是圆x2+y2=4的切线
∴点O(0,0)到直线的距离为d=$\frac{|-2k+2|}{\sqrt{1+{k}^{2}}}$=2,解之得k=0
此时直线方程为y=2,
∴切线方程为y=2或x=2.
故答案为:y=2或x=2.
点评 借助于求过圆外一个定点的圆的切线方程的问题,考查了直线与圆的位置关系、点到直线的距离公式等知识点,属于基础题.


科目:高中数学 来源: 题型:解答题
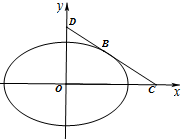 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),离心率e=$\frac{{\sqrt{2}}}{2}$,且过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),离心率e=$\frac{{\sqrt{2}}}{2}$,且过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,n∥α,则m⊥α | B. | 若m∥β,β⊥α则m⊥α | ||
| C. | 若m∥n,n⊥α则m⊥α | D. | 若m⊥n,n⊥β,β⊥α,则m⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -p | C. | -$\frac{p}{2}$ | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com