练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知（b-c）logmx+（c-a）logmy+（a-b）logmz=0.

    （1）设a，b，c依次成等差数列，且公差不为0.

    求证：x，y，z成等比数列.

    （2）设正数x，y，z依次成等比数列，且公比不为1.求证：a，b，c成等差数列.

    解：（1）∵a，b，c成等差数列，且公差d≠0，

    ∴b-c=a-b=-d，c-a=2d.

    代入已知条件，得

    -d（logmx-2logmy+logmz）=0.

    ∴logmx-2logmy+logmz=0.

    logmx+logmz=2logmy，即logmxz=logmy2.

    ∴y2=xz.

    又x，y，z都是正数，∴x，y，z成等比数列.

    （2）∵x，y，z成等比数列，且公比q≠1，

    ∴y=xq，z=xq2.把它们都代入已知条件，得

    （b-c）logmx+（c-a）logmxq+（a-b）logmxq2=0.

    整理，得（c+a-2b）logmq=0.

    其中q≠1，∴logmq≠0，∴c+a-2b=0，

    即2b=a+c.

    因此，a，b，c成等差数列.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)＝log(3x2－ax＋5)在[－1，＋∞)上是减函数，则实数a的取值范围是(　　)

    A．－8≤a≤－6   B．－8<a<－6

    C．－8<a≤－6    D．a≤－6

    查看答案和解析>>

    科目：高中数学 来源：2014届山东省聊城市高二第四次模块检测理科数学卷（解析版） 题型：选择题

    已知a,b,a+b成等差数列,a,b,ab成等比数列,且0<log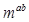<1,则m的取值范围是（   ）

    A．m>1                                 B．1<m<8

    C．m>8                                 D．0<m<1或m>8

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江西师大附中高三（上）10月月考数学试卷（文科）（解析版） 题型：选择题

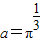    已知，b=logπ3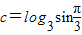，，则a，b，c大小关系为（ ）
    A．a＞b＞c
    B．b＞c＞a
    C．c＞a＞b
    D．c=a＞b

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省宁波市余姚三中高三（上）第一次月考数学试卷（文科）（解析版） 题型：选择题

    已知，b=logπ3，，则a，b，c大小关系为（ ）
    A．a＞b＞c
    B．b＞c＞a
    C．c＞a＞b
    D．c=a＞b

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年黑龙江省哈尔滨三中高三（上）9月月考数学试卷（文科）（解析版） 题型：选择题

    已知，b=logπ3，，则a，b，c大小关系为（ ）
    A．a＞b＞c
    B．b＞c＞a
    C．c＞a＞b
    D．c=a＞b

    查看答案和解析>>

    同步练习册答案