解:(1)①∵F(x)=f(x)-g(x)=x
2+ax+c-lnx-c=x
2+ax-lnx,
∴

,
∵函数F(x)在[1,2]上是减函数,
∴当x∈[1,2]时,

恒成立,即

恒成立,
又

,
∴a∈

;
②由G(x)=F(x)-x
2=x
2+ax-lnx-x
2=ax-lnx,
由

<0,得x<

,若
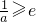
,则G(x)在(0,e]上为减函数,此时G(x)
min=ae-1,
由ae-1=3,得a=
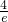
(舍);若
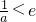
,则函数G(x)在(0,

)上为减函数,在(

,e)上为增函数,
所以

,由

,得a=e
2
所以存在a=e
2,使函数G(x)的最小值是3.
(2)令

,
则

,

,
∴

∴g(x)=0,
在(x
1,x
2)内必有一个实根.即?x
0∈(x
1,x
2),使

成立.
分析:(1)①求出函数F(x),由导函数在[1,2]上小于等于0恒成立,采用分离变量求a的范围;②求出函数G(x),求其导函数,分最小值在不在给定的区间两种情况讨论a的存在性;
(2)构造函数

,判出g(x
1)•g(x
2)<0,则说明?x
0∈(x
1,x
2),使

成立.
点评:本题(1)考查了利用函数的导函数判断函数的单调性以及函数零点的判断,考查了运用导函数的符号判断函数单调性的方法,同时考查了分类讨论的数学思想;
(2)考查了函数零点的判定,判断函数在某区间内有零点,只要满足区间两端点处的函数值的乘积小于0即可.

 成立.
成立. ,
, 恒成立,即
恒成立,即 恒成立,
恒成立, ,
, ;
; <0,得x<
<0,得x< ,若
,若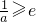 ,则G(x)在(0,e]上为减函数,此时G(x)min=ae-1,
,则G(x)在(0,e]上为减函数,此时G(x)min=ae-1,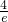 (舍);若
(舍);若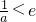 ,则函数G(x)在(0,
,则函数G(x)在(0, )上为减函数,在(
)上为减函数,在( ,e)上为增函数,
,e)上为增函数, ,由
,由 ,得a=e2
,得a=e2 ,
, ,
, ,
, ∴g(x)=0,
∴g(x)=0, 成立.
成立. ,判出g(x1)•g(x2)<0,则说明?x0∈(x1,x2),使
,判出g(x1)•g(x2)<0,则说明?x0∈(x1,x2),使 成立.
成立.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<