
 如图,边长为2的正方形ABCD外有一点P,且PA=PB=PC=PD=2中,E是PC的中点.
如图,边长为2的正方形ABCD外有一点P,且PA=PB=PC=PD=2中,E是PC的中点.| 1 |
| 2 |
| EB2-OB2 |
| OE |
| EB |

| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| EB2-OB2 |
| OE |
| EB |
| ||
| 3 |


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
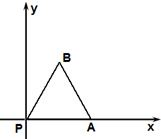 如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是
如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•洛阳一模)如图放置的边长为1的正三角形ABC沿x轴的正方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系是y=f(x).则f(x)在两个相邻零点间的图象与x轴围成的面积是
(2011•洛阳一模)如图放置的边长为1的正三角形ABC沿x轴的正方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系是y=f(x).则f(x)在两个相邻零点间的图象与x轴围成的面积是| 2π |
| 3 |
| ||
| 4 |
| 2π |
| 3 |
| ||
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.查看答案和解析>>
科目:高中数学 来源: 题型:
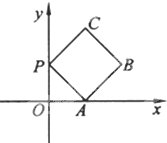 如图放置的边长为2的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),则f(x)的最小正周期为
如图放置的边长为2的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),则f(x)的最小正周期为查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省四校联考高三(上)期末数学试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com