Question

已知函数为常数），数列{a_n}满足：，a_n+1=f（a_n），n∈N*．
（1）当α=1时，求数列{a_n}的通项公式；
（2）在（1）的条件下，证明对?n∈N*有：；
（3）若α=2，且对?n∈N*，有0＜a_n＜1，证明：．

Answer 1

解：（1）当α=1时，，两边取倒数，得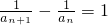，----（2分）
故数列是以为首项，1为公差的等差数列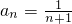，，，n∈N*．--------------（4分）
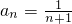（2）证法1：由（1）知，故对k=1，2，3…=-------------（6分）
∴a₁a₂a₃+a₂a₃a₄+…+a_na_n+1a_n+2
=
==．------------------------------（9分）．
[证法2：①当n=1时，等式左边=，
等式右边=，左边=右边，等式成立；-------------------------（5分）
②假设当n=k（k≥1）时等式成立，
即，
则当n=k+1时
=
=
这就是说当n=k+1时，等式成立，----------------------------------------（8分）
综①②知对于?n∈N*有：．----（9分）]
（3）当α=2时，则，-------------------（10分）
∵0＜a_n＜1，
∴--------------------------------（11分）===．--------------------（13分）
∵a_n=1-a_n与不能同时成立，∴上式“=”不成立，
即对?n∈N^*，．-----------------------------------------------------------（14分）
证法二：当α=2时，，
则----------------------------------------------------（10分）
又0＜a_n＜1，∴，
∴a_n+1＞a_n，∴a_n∈[，1），n∈N^*------------------------------------------------（11分）
令，则，--------------------------（12分）
当，所以函数g（x）在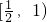单调递减，故当，所以命题得证------------------（14分）
所以命题得证-----------------------------------------（14分）
分析：（1）当α=1时，说明数列是以为首项，1为公差的等差数列，然后求数列{a_n}的通项公式；
（2）法一：在（1）的条件下，化简数列的通项公式，利用裂项法：证明对?n∈N*有：；
法二：直接利用数学归纳法的证明步骤证明即可．
（3）法一：通过α=2，化简a_n+1-a_n的表达式为，利用基本不等式直接证明．
法二：通过，以及0＜a_n＜1，说明，a_n∈[，1），n∈N^*，构造函数，利用函数的导数，求出函数的最大值即可证明结果．
点评：本题考查数列与函数的综合应用，数学归纳法的证明方法，构造法以及函数的导数求解函数的最大值证明不等式，基本不等式的应用，考查分析问题解决问题的能力，转化思想的应用．