
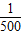 ,只需求出可行域直线在y轴上的截距最大值即可.
,只需求出可行域直线在y轴上的截距最大值即可.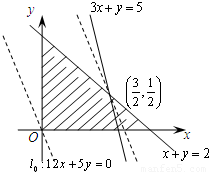 解:设这位农民种水稻x亩,种花生y亩,
解:设这位农民种水稻x亩,种花生y亩,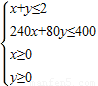 即
即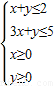 …(6分)
…(6分)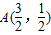 时,利润z取得最大值.…(11分)
时,利润z取得最大值.…(11分) 亩,种花生
亩,种花生 亩时可以得到最大利润.…(12分)
亩时可以得到最大利润.…(12分)

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
一农民有田2亩,根据他的经验:若种水稻,则每亩每期产量为400公斤,若种花生,则每亩产量为100公斤,但水稻成本较高,每亩每期240元,而花生只要80元,且花生每公斤可卖5元,稻米每公斤只卖3元,现在他只能凑足400元,问这位农民对两种作物应各种多少亩,才能得到最大利润?
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:广东省月考题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com