
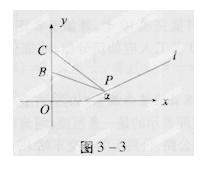
某人在一山坡P处观看对面山崖顶上的一座铁塔.如图所示,塔及所在的山崖可视为图中的竖直线OC,塔高BC=80(米),山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为α,tanα=![]() .试问,此人距山崖的水平距离多远时,观看塔的视角∠BPC最大(不计此人的身高)?
.试问,此人距山崖的水平距离多远时,观看塔的视角∠BPC最大(不计此人的身高)?

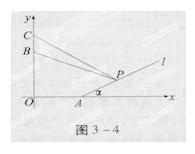
[考场错解] 如图所示,建立平面直角坐标系,则A(200,0),B(0,220),C(0,300)
直线l的方程为y=(x-200)tanα,即y=![]() .设此人距山崖的水平距离为x,
.设此人距山崖的水平距离为x,
 则P(x,
则P(x,![]() )(x>200),由经过两点的直线的斜率公式
)(x>200),由经过两点的直线的斜率公式
kPC=![]() =
=![]() kPB=
kPB=![]() .由直线PC到直线PB的角的公式得:
.由直线PC到直线PB的角的公式得:
tan ∠BPC=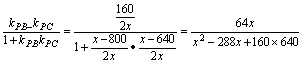
设u=![]() ∴ux2-(288u-64)x+160×640u=0 ①
∴ux2-(288u-64)x+160×640u=0 ①
∵u≠0∵x∈R.△=(288u-64)2-4×160×640u2≥0. 解得 u≤2.
 当u=2时,x=320.即此人距山崖320米时,观看铁塔的视角∠BPC最大.
当u=2时,x=320.即此人距山崖320米时,观看铁塔的视角∠BPC最大.
[专家把脉] 上述解答过程中利用x∈R由判别式法求u的最大值是错误的,因为x>200,即由判别式求得u的最大值,还必须检验方程①的根在(200,+∞)内.
[对症下药] 如图所示,建立平面直角坐标系,则A(200,0),B(0,220),C(0,300).直线l的方程为y=(x-200)tanα,即y=![]() .
.
设此人距山崖的水平距离为x,则P(x,![]() )(x>200).由经过两点的直线的斜率公式
)(x>200).由经过两点的直线的斜率公式
kPC=![]() ,kPB=
,kPB=![]() .由直线PC到直线PB的角的公式得
.由直线PC到直线PB的角的公式得
tan∠BPC=![]() =
=![]()
要使tan∠BPC达到最大,只须x+![]() 达到最小.由均值不等式
达到最小.由均值不等式
x+![]() ≥2
≥2![]() ,当且仅当x=
,当且仅当x=![]() 时上式取得等号.故当x=320时tan∠BPC最大.由此实际问题知,0<∠BPC<
时上式取得等号.故当x=320时tan∠BPC最大.由此实际问题知,0<∠BPC<![]() ,所以tan∠BPC最大时,∠BPC最大,故当此人距山崖水平距离为320米时,观看铁塔的视角∠BPC最大.
,所以tan∠BPC最大时,∠BPC最大,故当此人距山崖水平距离为320米时,观看铁塔的视角∠BPC最大.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
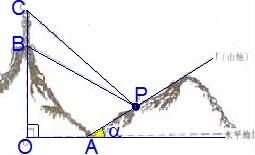 某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔及所在的山崖可视为图中的竖线OC,塔高BC?80(米),山高OB?220(米),OA?200(米),图中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为α,tanα=
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔及所在的山崖可视为图中的竖线OC,塔高BC?80(米),山高OB?220(米),OA?200(米),图中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为α,tanα=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某人在一山坡P处观看对面山顶上的一座铁塔,如图所示,塔高BC=40(米),塔所在的山高OB=290(米),OA=210(米),图中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为α,tanα=
某人在一山坡P处观看对面山顶上的一座铁塔,如图所示,塔高BC=40(米),塔所在的山高OB=290(米),OA=210(米),图中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为α,tanα=| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源:2008-2009学年湖北省武汉二中高一(下)期末数学试卷(文科)(解析版) 题型:解答题
 .试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高).
.试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高).
查看答案和解析>>
科目:高中数学 来源:2012-2013学年新课标高三(上)数学一轮复习单元验收7(理科)(解析版) 题型:解答题
 .试问,此人距山崖的水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?
.试问,此人距山崖的水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?
查看答案和解析>>
科目:高中数学 来源:2011年云南省高三数学一轮复习单元测试04:三角函数(解析版) 题型:解答题
 .试问,此人距山崖的水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?
.试问,此人距山崖的水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com