Question

设等比数列{a_n}的公比为q,前n项和S_n＞0(n=1,2,…).

(1)求q的取值范围;

(2)设b_n=a_n+2-a_n+1,记{b_n}的前n项和为T_n,试比较S_n和T_n的大小.

Answer 1

解：(1)因为{a_n}是等比数列,S_n＞0,

可得a₁=S₁＞0,q≠0.

当q=1时,S_n=na₁＞0;

当q≠1时,S_n=＞0,

即＞0(n=1,2,…).

上式等价于不等式组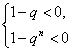(n=1,2,…)        ①

或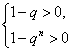(n=1,2,…).                              ②

解①式得q＞1;解②,由于n可为奇数,可为偶数,得-1＜q＜1.

综上,q的取值范围是(-1,0)∪(0,+∞).

(2)由b_n=a_n+2-a _n+1,得

b_n=a_n(q²-q),T_n=(q²-q)S_n.

于是T_n-S_n=S_n(q²-q-1)=S_n(q+)(q-2).

又因为S_n＞0,且-1＜q＜0或q＞0,所以,

当-1＜q＜-或q＞2时,T_n-S_n＞0,即T_n＞S_n;

当-＜q＜2且q≠0时,T_n-S_n＜0,即T_n＜S_n;

当q=-或q=2时,T_n-S_n=0,即T_n=S_n.