
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
API |
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为w)的关系式为:
 ,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染完成下面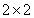 列联表,并判断能否有
列联表,并判断能否有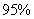 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
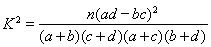
| 非重度污染 | 重度污染 | 合计 |
供暖季 |
|
|
|
非供暖季 |
|
|
|
合计 |
|
| 100 |
(1)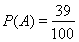 ;(2)有95%的把握认为空气重度污染与供暖有关
;(2)有95%的把握认为空气重度污染与供暖有关
【解析】
试题分析:(1)根据所给数据,求出经济损失S大于200元且不超过600元的天数的频率,以此频率作为“在本年内随机抽取一天,该天经济损失S大于200元且不超过600元”的概率(估计)
(2)由于总共有15天为重度污染,其中有8天在供暖季,那么有7天在非供暖季;在30天供暖季中有8天为重度污染,那么有22天为非重度污染;非重度污染有85天其中有22天在供暖季,那么有63天在非供暖季,由此可完成 列联表:
列联表:
| 非重度污染 | 重度污染 | 合计 |
供暖季 | 22 | 8 | 30 |
非供暖季 | 63 | 7 | 70 |
合计 | 85 | 15 | 100 |
代入公式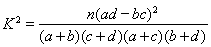 即可求得K2的观测值,从而确定是否有95%的把握认为空气重度污染与供暖有关
即可求得K2的观测值,从而确定是否有95%的把握认为空气重度污染与供暖有关
试题解析:(1)设“在本年内随机抽取一天,该天经济损失S大于200元且不超过600元”为事件A
1分
由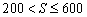 ,得
,得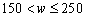 ,频数为39, 3分
,频数为39, 3分
所以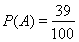 4分
4分
(2)根据以上数据得到如下列联表:
| 非重度污染 | 重度污染 | 合计 |
供暖季 | 22 | 8 | 30 |
非供暖季 | 63 | 7 | 70 |
合计 | 85 | 15 | 100 |
8分
K2的观测值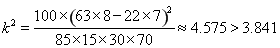 10分
10分
所以有95%的把握认为空气重度污染与供暖有关 12分
考点:1、概率与统计;2、函数的应用


科目:高中数学 来源: 题型:
| 组别 | PM2.5浓度 (微克/立方米) |
频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100) | 2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•湖北模拟)城市的空气质量以其空气质量指数API(为整数)衡量,指数越大,级别趁高,说明污染越严重,对人体健康的影响也越明显.根据空气质级指数.API的不同,可将空气质盘分级如下表:
(2012•湖北模拟)城市的空气质量以其空气质量指数API(为整数)衡量,指数越大,级别趁高,说明污染越严重,对人体健康的影响也越明显.根据空气质级指数.API的不同,可将空气质盘分级如下表:| API | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 | 251~300 | >300 |
| 状况 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
| API分组 | [41,51) | [51,61) | [61,71) | [71,81) | [81,91) | [91,101) | [101,111) |
| 频数 | 2 | 1 | 4 | 6 | 10 | 5 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.查看答案和解析>>
科目:高中数学 来源:2013-2014学年哈师大、东北师大、辽宁实验中学高三第一次联合模拟文数学卷(解析版) 题型:解答题
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
API |
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为w)的关系为:
 ,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染完成下面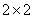 列联表,并判断能否有
列联表,并判断能否有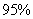 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
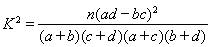
| 非重度污染 | 重度污染 | 合计 |
供暖季 |
|
|
|
非供暖季 |
|
|
|
合计 |
|
| 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com