
 某企业生产一种汽车配件,经抽样统计,该企业生产的配件尺寸的样本频率分布直方图如下.配件尺寸在[60,62)内的为一等品,尺寸在[58,60)或[62,64)内的为二等品,其余为三等品.用频率近似表示概率.
某企业生产一种汽车配件,经抽样统计,该企业生产的配件尺寸的样本频率分布直方图如下.配件尺寸在[60,62)内的为一等品,尺寸在[58,60)或[62,64)内的为二等品,其余为三等品.用频率近似表示概率.

科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x(件) | 3 | 4 | 5 | 6 |
| y(万元) | 2.5 | 3 | 4 | 4.5 |
 |
| y |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
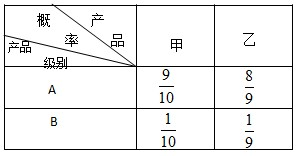 (2010•合肥模拟)某企业生产一种风险较大的高科技产品M,要用甲和乙两种初级产品组合而成,甲和乙两种初级产品生产相互独立,每种初级产品生产结果均有A、B两个等级. 若随机的选用甲、乙两种初级产品各一个组装成一个产品M,甲和乙两种初级产品均为A级时组合而成产品M为合格品,其余均为次品.该厂在生产甲和乙两种初级产品时的等级概率如表:
(2010•合肥模拟)某企业生产一种风险较大的高科技产品M,要用甲和乙两种初级产品组合而成,甲和乙两种初级产品生产相互独立,每种初级产品生产结果均有A、B两个等级. 若随机的选用甲、乙两种初级产品各一个组装成一个产品M,甲和乙两种初级产品均为A级时组合而成产品M为合格品,其余均为次品.该厂在生产甲和乙两种初级产品时的等级概率如表:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com