
 (n∈N*)的所有项按照从大到小的原则写成如图所示的数表,其中的 第k行有2k-1个数,第k行的第s个数(从左数起)记为A(k,s),则A(5,12)表示的数是 ;
(n∈N*)的所有项按照从大到小的原则写成如图所示的数表,其中的 第k行有2k-1个数,第k行的第s个数(从左数起)记为A(k,s),则A(5,12)表示的数是 ; 这个数可记为A( ).
这个数可记为A( ).
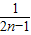 可知,每一行数的分母成等差数列,可求A(k,s),令k=5,s=12,可求A(5,12)
可知,每一行数的分母成等差数列,可求A(k,s),令k=5,s=12,可求A(5,12)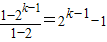 个数,
个数,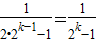 ,
,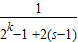 ,
,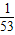 ;
;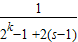 =
=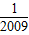 ,
,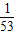 ;10,494.
;10,494.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
| Sn |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 把数列
把数列 (n∈N*)的所有项按照从大到小的原则写成如图所示的数表,其中的 第k行有2k-1个数,第k行的第s个数(从左数起)记为A(k,s),则A(5,12)表示的数是 ________;
(n∈N*)的所有项按照从大到小的原则写成如图所示的数表,其中的 第k行有2k-1个数,第k行的第s个数(从左数起)记为A(k,s),则A(5,12)表示的数是 ________; 这个数可记为A( ________).
这个数可记为A( ________).查看答案和解析>>
科目:高中数学 来源:《第2章 数列》2010年单元测试卷(1)(解析版) 题型:填空题
 (n∈N*)的所有项按照从大到小的原则写成如图所示的数表,其中的 第k行有2k-1个数,第k行的第s个数(从左数起)记为A(k,s),则A(5,12)表示的数是 ;
(n∈N*)的所有项按照从大到小的原则写成如图所示的数表,其中的 第k行有2k-1个数,第k行的第s个数(从左数起)记为A(k,s),则A(5,12)表示的数是 ; 这个数可记为A( ).
这个数可记为A( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com