
(1)起初,两人的距离是多少?
(2)用包含t的式子表示t小时后两人的距离;
(3)什么时候两人的距离最短?

思路分析:本题是已知两边夹角求第三边的简单应用问题,但是在第(2)小问要对动态中的P和Q分0≤t≤![]() 和t>
和t>![]() 两种情况讨论,最后统一成一种表达式.
两种情况讨论,最后统一成一种表达式.
解:(1)设甲、乙两人最初的位置是A、B,
则|![]() |2=|
|2=|![]() |2+|
|2+|![]() |2-2|
|2-2|![]() ||
||![]() |cos60°=32+12-2×3×1×
|cos60°=32+12-2×3×1×![]() =7,
=7,
∴|![]() |=7(km).
|=7(km).
(2)设甲、乙两人t小时后的位置分别是P、Q,则|AP|=4t,|BQ|=4t.
当0≤t≤![]() 时,|
时,|![]() |2=(3-4t)2+(1+4t)2-2(3-4t)(1+4t)cos60°;
|2=(3-4t)2+(1+4t)2-2(3-4t)(1+4t)cos60°;
当t>![]() 时,|
时,|![]() |2=(4t-3)2+(1+4t)2-2(4t-3)(1+4t)cos120°.
|2=(4t-3)2+(1+4t)2-2(4t-3)(1+4t)cos120°.
注意到,上面两式实际上是统一的,所以|![]() |2=48t2-24t+7,
|2=48t2-24t+7,
即|![]() |=48t2-24t+7.
|=48t2-24t+7.
(3)∵|![]() |2=48(t-
|2=48(t-![]() )2+4,
)2+4,
∴当t=![]() h时,即在第15 min末,PQ最短,最短距离是2 km.
h时,即在第15 min末,PQ最短,最短距离是2 km.
方法归纳 本题甲可以在O点的左侧或右侧,故需分类讨论.不论哪种情况最后结果的结构和形式是相同的.另外求最值的问题,往往要引入变量,建立函数关系式进一步转化成常见函数的最值.


科目:高中数学 来源: 题型:
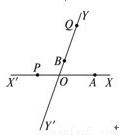
 如图所示,有两条相交成60°角的直线xx′,y′y,交点是O,甲、乙分别在ox,oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′的方向,乙沿y′y的方向步行.
如图所示,有两条相交成60°角的直线xx′,y′y,交点是O,甲、乙分别在ox,oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′的方向,乙沿y′y的方向步行.查看答案和解析>>
科目:高中数学 来源: 题型:
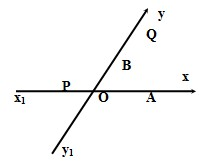 如图所示,有两条相交成60°的直路xx1,yy1,交点为O,甲、乙分别在Ox、Oy上,起初甲位于离O点3km的A处,乙位于离O点1km的B处.后来两人同时以每小时4km的速度,甲沿xx1的方向,乙沿y1y的方向. 求:(1)起初两人的距离是多少?(2)什么时候两人的距离最短?
如图所示,有两条相交成60°的直路xx1,yy1,交点为O,甲、乙分别在Ox、Oy上,起初甲位于离O点3km的A处,乙位于离O点1km的B处.后来两人同时以每小时4km的速度,甲沿xx1的方向,乙沿y1y的方向. 求:(1)起初两人的距离是多少?(2)什么时候两人的距离最短?查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,有两条相交成60°的直线xx′、yy′,其交点是O,甲、乙两辆汽车分别在xx′、yy′上行驶,起初甲离O点30 km,乙离O点10 km,后来两车均以60 km/h的速度,甲沿xx′方向,乙沿yy′方向行驶.
如图所示,有两条相交成60°的直线xx′、yy′,其交点是O,甲、乙两辆汽车分别在xx′、yy′上行驶,起初甲离O点30 km,乙离O点10 km,后来两车均以60 km/h的速度,甲沿xx′方向,乙沿yy′方向行驶.查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第4章 平面向量):4.6 向量的应用(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2014届四川省成都市六校协作体高一下学期期中联考数学试卷(解析版) 题型:解答题
如图所示,有两条相交成 角的直路
角的直路 ,
, ,交点是
,交点是 ,甲、乙分别在
,甲、乙分别在 ,
, 上,起初甲离
上,起初甲离 点
点 km,乙离
km,乙离 点
点 km,后来两人同时用每小时
km,后来两人同时用每小时 km的速度,甲沿
km的速度,甲沿 的方向,乙沿
的方向,乙沿 的方向步行.
的方向步行.
⑴起初,两人的距离是多少?
⑵用包含 的式子表示
的式子表示 小时后两人的距离;
小时后两人的距离;
⑶什么时候两人的距离最短?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com