
|
|
|
|
|
|
|
|
| y1-y2 |
| x1-x2 |


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=| 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数y=Asin(ωx+
如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数y=Asin(ωx+| 2π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
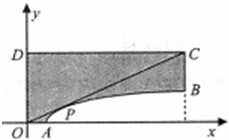 已知图形OAPBCD是由不等式组
已知图形OAPBCD是由不等式组
|
查看答案和解析>>
科目:高中数学 来源: 题型:
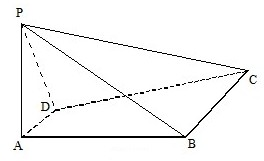 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建师大附中高二(上)期末数学试卷(文科)(解析版) 题型:解答题
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形, ,|AN|=3,且|BN|=6.
,|AN|=3,且|BN|=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com