
思路分析:我们可以按照从特殊到一般的证明思路.首先证明三角形与其投影具有两公共顶点.然后再证一般情况.
证明:(1)如图
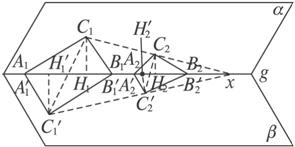
图
∵C1与C1′,C2与C2′是射影对应点,
∴C
由这些点向对应轴直线g作垂线C1H1,C1′H1′,C2H2,C2′H2′.
设C
![]() =
=![]() ,
,![]() =
=![]() .
.
∵C![]() =
=![]() =
=![]() =k时,
=k时,
![]() =
=![]() =k.
=k.
又∵△A1B
∴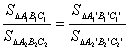 或
或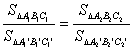 =k,
=k,
其中k为常数.
(2)当三角形与其射影没有公共顶点时,如图
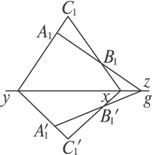
图
在△A1B
由(1)中结论知:
![]() =k,即
=k,即![]() =k
=k![]() .
.
![]() =k,即
=k,即![]() =k
=k![]() .
.
![]() =k,即
=k,即![]() =k
=k![]() .
.
∴![]() =
=![]() +
+![]() -
-![]() =k
=k![]() +k
+k![]() -k
-k![]() =k(
=k(![]() +
+![]() -
-![]() )=k
)=k![]() .
.
∴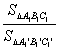 =k.同理,
=k.同理,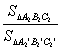 =k,
=k,
∴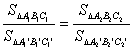 .
.


科目:高中数学 来源: 题型:
| S△OM1N1 |
| S△OM2N2 |
| OM1 |
| OM2 |
| ON1 |
| ON2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| (n-2)(n+1) |
| 2 |
| (n-2)(n+1) |
| 2 |
| S△OM1N1 |
| S△OM2 N2 |
| OM1 |
| OM2 |
| ON1 |
| ON2 |
| VO-P1Q1R1 |
| VO-P2Q2R2 |
| OP1•OQ1•OR1 |
| OP2•OQ2•OR2 |
| OP1•OQ1•OR1 |
| OP2•OQ2•OR2 |
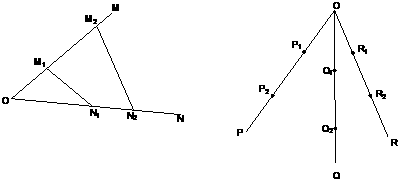
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
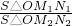 =
=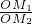 =
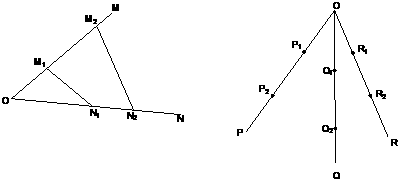
=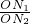 ,若不在同一平面内的射线OP,OQ和OR上分别存在点P1P2,点Q1Q2和点R1R2,则
,若不在同一平面内的射线OP,OQ和OR上分别存在点P1P2,点Q1Q2和点R1R2,则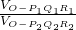 =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年广东省实验中学高二(下)期中数学试卷(文科)(解析版) 题型:解答题
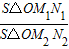 =
=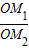 =
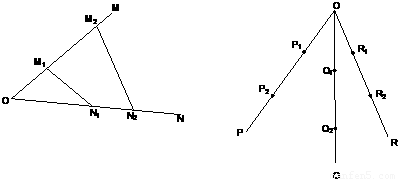
=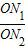 ,若不在同一平面内的射线OP,OQ和OR上分别存在点P1P2,点Q1Q2和点R1R2,则
,若不在同一平面内的射线OP,OQ和OR上分别存在点P1P2,点Q1Q2和点R1R2,则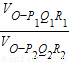 =______.
=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com