
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
(1)求证:AF∥平面BCE;
(2)若∠CAD=90°,求三棱锥F-BCE的体积.
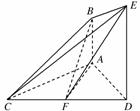
解:(1)证法一:如图1,取DE的中点M,连接AM,FM,
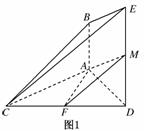
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE.
又∵AB=EM=![]() DE,
DE,
∴四边形ABEM是平行四边形,
∴AM∥BE.
又∵AM⊄平面BCE,BE⊂平面BCE,
∴AM∥平面BCE.
∵CF=FD,DM=M![]() E,∴MF∥CE,
E,∴MF∥CE,
又∵MF⊄平面BCE,CE⊂平面BCE,
∴MF∥平面BCE,又∵AM∩MF=M,
∴平面AMF∥平面BCE,
∵AF⊂平面AMF,∴AF∥平面BCE.
证法二:如图2,取CE的中点N,连接FN,BN.
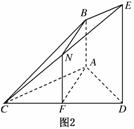
∵AB⊥平面ACD,DE⊥平面ACD,∴AB∥DE,
∵CF=FD,CN=NE,∴NF∥DE,NF=![]() DE,
DE,
又AB=![]() DE,∴AB∥NF,AB=NF,
DE,∴AB∥NF,AB=NF,
∴四边形ABNF是平行四边形,∴AF∥BN,
又∵AF⊄平面BCE,BN⊂平面BCE,∴AF∥平面BCE.
(2)由(1),知AF∥平面BCE,∴VF-BCE=VA-BCE=VC-ABE.
∵AB⊥平面ACD,∴平面ABED⊥平面ACD,
∵∠CAD=90°,即AC⊥AD,
∴AC⊥平面ABED,所以,AC是三棱锥C-ABE的高.
∵AB=2,AD=4,∴S△ABE=![]() AB·AD=
AB·AD=![]() ×2×4=4.
×2×4=4.
∴VC-ABE=![]() S△ABE·AC=
S△ABE·AC=![]() ×4×4=
×4×4=![]() .
.
另解:VF-BCE=VB-CFE=![]() (
(![]() ×2
×2![]() ×4)×2
×4)×2![]() =
=![]() .
.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
 (2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com