
当![]() 为何值时,直线
为何值时,直线![]() 在两坐标轴上的截距相等.
在两坐标轴上的截距相等.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(1)过点![]() 与双曲线
与双曲线![]() 有且只有一个公共点的直线有几条,分别求出它们的方程。
有且只有一个公共点的直线有几条,分别求出它们的方程。
(2)直线![]() 与双曲线
与双曲线![]() 相交于A、B两点,当
相交于A、B两点,当![]() 为何值时,A、B在双曲线的同一支上?当
为何值时,A、B在双曲线的同一支上?当![]() 为何值时,A、B分别在双曲线的两支上?
为何值时,A、B分别在双曲线的两支上?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省兴化市高三12月月考数学试卷(解析版) 题型:解答题
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路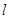 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数 的图象,且点M到边OA距离为
的图象,且点M到边OA距离为 .
.

(1)当 时,求直路
时,求直路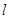 所在的直线方程;
所在的直线方程;
(2)当 为何值时,地块OABC在直路
为何值时,地块OABC在直路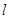 不含泳池那侧的面积取到最大,最大值是多少?
不含泳池那侧的面积取到最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源:2012届福建省六校联考上学期高三第三次月考文科数学试卷 题型:解答题
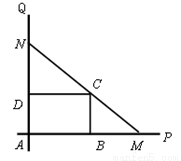
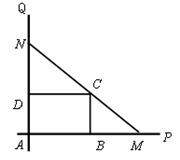
如下图,互相垂直的两条公路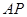 、
、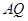 旁有一矩形花园
旁有一矩形花园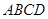 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园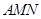 ,要求点
,要求点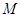 在射线
在射线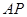 上,点
上,点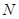 在射线
在射线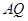 上,且直线
上,且直线 过点
过点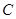 ,其中
,其中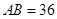 米,
米, 米. 记三角形花园
米. 记三角形花园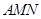 的面积为
的面积为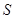 .
.
(Ⅰ)当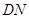 为何值时,
为何值时,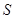 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(Ⅱ)若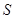 不超过1764平方米,求
不超过1764平方米,求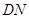 长的取值范围.
长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
如下图,互相垂直的两条公路![]() 、
、![]() 旁有一矩形花园
旁有一矩形花园![]() ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园![]() ,要求点
,要求点![]() 在射线
在射线![]() 上,点
上,点![]() 在射线
在射线![]() 上,且直线
上,且直线![]() 过点
过点![]() ,其中
,其中![]() 米,
米,![]() 米. 记三角形花园
米. 记三角形花园![]() 的面积为
的面积为![]() .
.
(Ⅰ)当![]() 为何值时,
为何值时,![]() 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(Ⅱ)若![]() 不超过1764平方米,求
不超过1764平方米,求![]() 长的取值范围.
长的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com