练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数f(x)=1+有反函数,且点M(a,b)既在函数f(x)的图象上,又在f-1 (x)的图象上,求a、b的值.

    思路解析:有两种思路:一是求出反函数,将点M(a,b)坐标分别代入原函数和反函数中去,从而求出a,b的值；二是根据互为反函数图象间的关系知,M(a,b)在f-1 (x)的图象上,则M′(b,a)在原函数的图象上,从而不求

    f-1 (x)而求出a,b的值.

    解法一:先求出f(x)的反函数.

    由y=1+(x≥),

    得f-1 (x)= (x-1)2+(x≥1).

    点M(a,b)在f(x)的图象上,有b=1+.

    又点M(a,b)在f-1 (x)的图象上,

    有b= (a-1)2+.由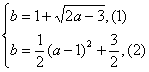

    消去b,得1+= (a-1)2+.

    化简,得(a-1)4+2(a-1)2-8(a-1)+5=0.

    因式分解,得［(a-1)-1］2［(a-1)2+2(a-1)+5］=0.

    ∵(a-1)2+2(a-1)+5≠0,∴(a-1)-1=0.

    ∴a=2.把a=2代入①式,得b=2.∴a=b=2.

    解法二:由点M在f(x)的图象上,得b=1+.

    ∵点M(a,b)在f-1 (x)的图象上,∴点M′(b,a)在f(x)的图象上.

    把点M′(b,a)代入y=1+得a=1+.

    ∴∴

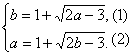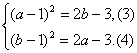
    ③-④,得［(a-1)+(b-1)］［(a-1)-(b-1)］=2(b-a).

    整理,得(a-b)(a+b)=0,于是a=b,或a=-b.

    将a=b代入①,得a=b=2.

    将a=-b代入①,得b2=-4(舍去).

    ∴a=b=2.

    深化升华

    在解法二中,由点M(a,b)在f-1 (x)的图象上,得点M关于y=x的对称点M′(b,a)在f(x)的图象上,可以避免求f(x)的反函数.

    解法二是本类题型的最佳解法.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （1）、已知函数f(x)=
    1+
    		2
    cos(2x-
    π
    4
    )
    sin(x+
    π
    2
    )
    ．若角α在第一象限且cosα=
    3
    5
    ，求f(α)    ．
    （2）函数f(x)=2cos2x-2
    		3
    sinxcosx    的图象按向量
    m
    =(
    π
    6
    ，-1)    平移后，得到一个函数g（x）的图象，求g（x）的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=(1-
    a
    x
    )ex    ，若同时满足条件：
    ①?x0∈（0，+∞），x0为f（x）的一个极大值点；
    ②?x∈（8，+∞），f（x）＞0．
    则实数a的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    1+lnx
    x
    ．
    （1）如果a＞0，函数在区间(a，a+
    1
    2
    )    上存在极值，求实数a的取值范围；
    （2）当x≥1时，不等式f(x)≥
    k
    x+1
    恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    1+
    1
    x
    ，(x＞1)
    x2+1，(-1≤x≤1)
    2x+3，(x＜-1)
    ．
    （1）求f(
    1
    		2
    -1
    )    与f（f（1））的值；
    （2）若f(a)=
    3
    2
    ，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义在D上的函数f（x）如果满足：对任意x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界．已知函数f(x)=
    1-m•2x1+m•2x
    ．
    （1）m=1时，求函数f（x）在（-∞，0）上的值域，并判断f（x）在（-∞，0）上是否为有界函数，请说明理由；
    （2）若函数f（x）在[0，1]上是以3为上界的有界函数，求m的取值范围．

    查看答案和解析>>

    同步练习册答案