
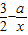 (a为实常数)
(a为实常数) ,1]上有解,求实数a的取值范围;
,1]上有解,求实数a的取值范围;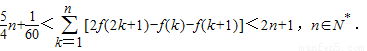 (参考数据:ln2≈0.6931)
(参考数据:ln2≈0.6931)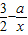 ,我们易求出当a=1时,函数φ(x)的解析式及其导函数的解析式,利用导数法,判断出函数的单调性,即可得到当x=4时,φ(x)取最小值;
,我们易求出当a=1时,函数φ(x)的解析式及其导函数的解析式,利用导数法,判断出函数的单调性,即可得到当x=4时,φ(x)取最小值; ,1]上有解,可转化为方程a=
,1]上有解,可转化为方程a=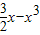 在区间[
在区间[ ,1]上有解,构造函数h(x)=
,1]上有解,构造函数h(x)=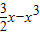 ,x∈[
,x∈[ ,1],利用导数法求出函数的值域,即可得到实数a的取值范围,
,1],利用导数法求出函数的值域,即可得到实数a的取值范围,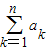 ≥
≥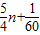 ,构造函数F(x)=lnx-x+2(x≥4)利用导数法,可以判断出函数的单调性,进而判断出
,构造函数F(x)=lnx-x+2(x≥4)利用导数法,可以判断出函数的单调性,进而判断出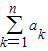 <2n+1,综合讨论结果,即可得到结论.
<2n+1,综合讨论结果,即可得到结论.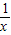 -
- ,
,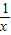 -
-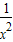 =
=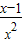 ,
, .(4分)
.(4分) ,1]上有解
,1]上有解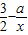 在区间[
在区间[ ,1]上有解
,1]上有解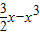 在区间[
在区间[ ,1]上有解
,1]上有解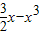 ,x∈[
,x∈[ ,1],
,1],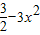 ,
, ,
,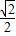 ]上,h′(x)≥0,在区间[
]上,h′(x)≥0,在区间[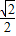 ,1]上,h′(x)≤0,
,1]上,h′(x)≤0, ,
,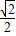 ]上单调递增,在区间[
]上单调递增,在区间[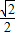 ,1]上单调递减,
,1]上单调递减, ).
).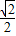 )
) ≤h(x)≤
≤h(x)≤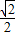
 ,
,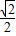 ]…(9分)
]…(9分)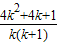 ,
, >0,
>0,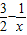 (x≥4)
(x≥4)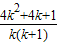 >4,
>4,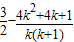 =
=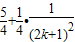 >
>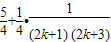 =
=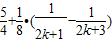 .
.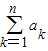 >
>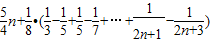 =
=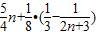 ≥
≥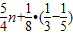 =
=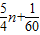
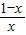 ,
,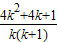 <4+
<4+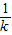 -
-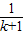 -2,
-2,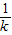 -
-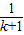 .
.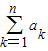 <2n+1-
<2n+1-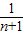 <2n+1.
<2n+1.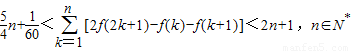 .(14分)
.(14分)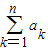 ≥
≥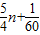 .本题综合了函数,导数,数列应用中的难点,难度较大.
.本题综合了函数,导数,数列应用中的难点,难度较大. 

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2(x-1) |
| x+1 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| a |
| ||
| x |
| 6 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com