练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知
    AB
    •
    BC
    +
    AB
    2    =0    ，则△ABC一定是
     
    三角形．
    分析：由
    AB
    •
    BC
    +
    AB
    2    =0    ，得：
    AB
    •(
    BC
    +
    AB
    ) =
    AB
     •
    AC
    =0    ，即：
    AB
    ⊥
    AC．
    得出答案．
    解答：解：由△ABC，
    AB
    •
    BC
    +
    AB
    2    = 0    ，
    得
    AB
    •(
    BC
    +
    AB
    )  =
    AB
    •
    AC
    =0    ，
    即
    AB
    ⊥
    AC，

    所以△ABC是直角三角形．
    故答案为直角．
    点评：通过向量的数量积为0得垂直关系，解题时经常用到．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

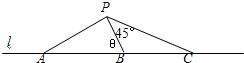    精英家教网如图，A，B，C是直线l上三点，P是直线l外一点，已知AB=BC=a，∠APB=90°，∠BPC=45°，记∠PBA=θ，则
    PA
    •
    PC
    =
     
    ．（用a表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在△ABC中，已知|
    AB
    |=4，|
    AC
    |=2，
    AD
    =
    1
    3
    AB
    +
    2
    3
    AC
    ，
    （1）证明：B，C，D三点共线；           （2）若|
    AD
    |=
    		6
    ，求|
    BC
    |    的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•湖北模拟）某地兴建一休闲商业广场，欲在如图所示的一块不规则用地规划建成一个矩形的商业楼区，余下作为休闲区域，已知AB⊥BC，OA∥BC，且AB=BC=2AO=4km，曲线段OC是以O为顶点且开口向上的抛物线的一段，如果要使矩形的相邻两边分别落在AB、BC上，且一个顶点落在曲线段OC上，应如何规划才能使矩形商业楼区的用地面积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2002•上海）如图所示，客轮以速度2v由A至B再到C匀速航行，货轮从AC的中点D出发，以速度v沿直线匀速航行，将货物送达客轮．已知AB=BC=50海里，若两船同时起航出发，则两船相遇之处距C点
    40.8
    40.8
    海里．（结果精确到小数点后1位）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网已知△ABC中，C是以AB为直径圆上一点，SA⊥平面ABC，AD⊥SC．
    （Ⅰ）求证：AD⊥平面SBC；
    （Ⅱ）已知SA=BC=3，AC=3
    		2
    ，求三棱锥S-ABC外接球体积V球．

    查看答案和解析>>

    同步练习册答案