
(1)求证:![]() ·
·![]() =
=![]() ·
·![]() .
.
(2)若l与双曲线C的左、右两支分别相交于点D、E,求双曲线C的离心率e的取值范围.
分析:根据条件写出l的方程,求出点P的坐标后,利用向量的坐标运算证明.
(1)证明:由题意知,直线l的方程为y=![]() (x-c).
(x-c).
由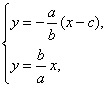
解得P(![]() ,
,![]() ).
).
∵|![]() |、|
|、|![]() |、|
|、|![]() |成等比数列.
|成等比数列.
∴xa·c=a2,∴xa=![]() ,∴A(
,∴A(![]() ,0).
,0).
∴![]() =(0,
=(0,![]() ),
),![]() =(
=(![]() ,
,![]() ),FP=(
),FP=(![]() ,
,![]() ).
).
∴![]() ·
·![]() =
=![]() ,
,![]() ·
·![]() =
=![]() .
.
∴![]() ·
·![]() =
=![]() ·
·![]() .
.
(2)解:由
得b2x2-![]() (x-c)2=a2b2,
(x-c)2=a2b2,
即(b4-a4)x2+2a4cx-(a4c2+a2b4)=0.
∵l与双曲线左、右两支分别相交于点D、E,设D(x1,y1),E(x2,y2),
∴x1·x2=![]() <0.∴b4>a4,即b2>a2,∴c2-a2>a2.
<0.∴b4>a4,即b2>a2,∴c2-a2>a2.
∴e2>2,即e>![]() .
.
点拨:解决离心率范围问题,就要构造出关于a、b、c的不等式进而求出e的范围,同时应注意e>1这一条件.


科目:高中数学 来源: 题型:
(2012年高考湖南卷理科5)已知双曲线C :![]() -
-![]() =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
A.![]() -
-![]() =1 B.
=1 B.![]() -
-![]() =1 C.
=1 C.![]() -
-![]() =1 D.
=1 D.![]() -
-![]() =1
=1
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广西南宁二中高三(下)5月月考数学试卷(文科)(解析版) 题型:解答题
 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为x=
,右准线方程为x=
查看答案和解析>>
科目:高中数学 来源:2014届湖南邵阳石齐学校高二第三次月考理科数学试卷(解析版) 题型:选择题
已知双曲线C :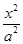 -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
)
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
)
A.  -
-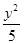 =1
B.
=1
B.  -
- =1 C.
=1 C.  -
- =1
D.
=1
D.  -
- =1
=1
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(湖南卷解析版) 题型:选择题
已知双曲线C : -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
A、 -
- =1 B、
=1 B、 -
- =1
C、
=1
C、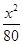 -
- =1
D、
=1
D、 -
- =1[w~#
=1[w~#
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com